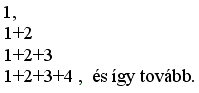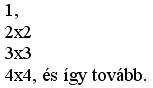Matematika/Hozzárendelhető segédletek/Tematikus tervezés

Az Alsós tanítói portálból

Az alábbiakban egy első osztályos tantervi témának - számtulajdonságok vizsgálata témán belül a páros-páratlan fogalma - egyfajta feldolgozási lehetőségét mutatjuk be. A  feldolgozáshoz munkalapokat mellékelünk. Ez a téma március, április táján kerül feldolgozásra.

Különböző számtulajdonságot vizsgálunk:

számok nagysága,

páros-páratlan fogalma,

számok kirakhatósága valahányasával, négyzetszámok, „lépcsős számok”, stb.

egyjegyű-kétjegyű számok,

számjegyek nagysága, alakulása műveletek elvégzése után

Tevékenységekkel, kirakásokkal, képolvasásokkal, rajzolással tehetjük szemléletessé a számtulajdonságokat. A tulajdonságok megtapasztalásakor egy-egy tulajdonsághoz hozzákeressük a rá jellemző számokat (a 20 körüli számkörben végzünk elsősorban megfigyeléseket). Most csak a páros-páratlan számtulajdonság feldolgozását emeljük ki.

A témához kapcsolódó feladatok

39.munkalap: Vágják ki a gyerekek a pénzeket és a négyzetlapokat. Ezek

hasznos eszközök, melyeket többször elővehetünk ennek a témakörnek a feldolgozása során. A pénzekkel, melyek lehetnek ‘Meseország” pénzei, kirakhatók a páros-páratlan számok, a 10-nél nagyobb számok, a csak 5-sel kirakható számok, stb. Vásárlásokat játszhatunk. A gyerekek ezekkel a pénzekkel fizetnek. (Lásd  az 50. munkalap kirakata)

A pénzekkel játszhatják a gyerekek a „Kettes, ötös játékot”, persze ezt számkártyákkal is lehet játszani. Sok kettes és ötös kell hozzá. Próbálják kirakni a számokat kettesekkel és ötösökkel. A 10-et két ötössel (5+5) vagy öt kettessel (2+2+2+2+2) könnyedén kirakja a kisgyerek. A 11 és 13 kirakása már nem könnyű. Sok kisgyerek azt hiszi, hogy nem is lehetséges. Próbálkozzanak! Majd rájön, hogy 6+5 az 11, tehát három kettes és egy ötös kell. Vessük fel, vajon az összes szám kirakható? Előbb-utóbb rájönnek, ha az 5-2-t visszakérek, megkapom a 3-at. Ha 5-bõl két kettest kérek vissza, az egyhez jutok. Adjunk a kezükbe sok 5-ös és 2-es számkártyát, kivonás és összeadás jeleket és próbáljuk összegyűjteni 1-tõl húszig az eseteket.

A négyzetlapokkal jól megjeleníthetők a lépcsős számok  (a matematikában háromszögszámként szerepelnek):

Megjeleníthetjük kirakással a négyzetszámokat is:

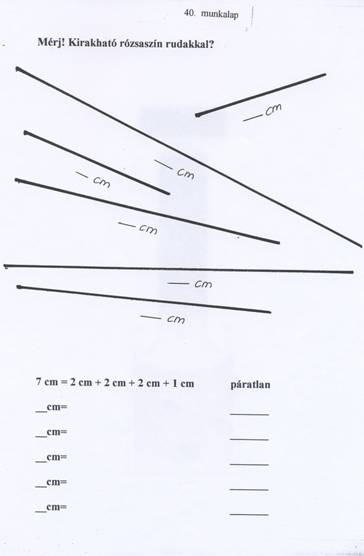
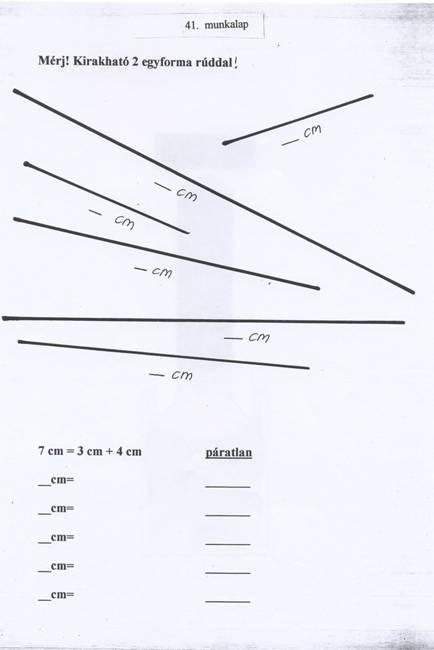
40-41. munkalap: A munkalapok használata előtt különböző számú gyerekcsoportok kialakításával vizsgálják meg, hogy tudnak-e párosával sorakozni vagy két egyenlő számú csoportot alakítani. 11 gyerek páratlan, mert sorakozáskor egy gyereknek nem jut pár. Azért is páratlan, mert a tornaversenyen az egyik csapatban eggyel több (vagy eggyel kevesebb) gyerek van.

A színes rudak közül a narancssárgát (a 10 cm-est) ki lehet rakni csupa 2 cm-es rózsaszín rúddal rakni, és két egyforma  citromsárga rúddal (5-5 cm) is lemérhetem. A munkalapokon lévő vonalakat is e szerint vizsgálják.

42.munkalap: Korongokkal, fehér kockákkal, termésekkel, pénzérmékkel vizs-gálhatják a kettesével és a két egyforma csoportbavaló kirakást. Az átrajzolás és az írásbeli lejegyzés ugyanennek a tevékenységnek az absztraktabb megjelenése. Sok tapasztalatot nyújtsunk a kisgyereknek a páros- páratlan számtulajdonsággal kapcsolatban.

Szervezhetünk olyan tevékenységeket is, ahol a páros és páratlan számú darabokat tükörrel nézegetjük. A 3 gomb páratlan számú. Mellé téve  a tükröt, 6 gombot látunk, ami páros szám lesz. A 8 gomb kétszerese 16 gomb lesz, a 8 páros tulajdonsága a kétszerezéskor is megmarad. Sok-sok tükrözés után jönnek rá a gyerekek, hogy tükörrel csak páros számokat tudnak előállítani.

Vizsgálják meg azt is, hogy mi történik, ha páros számhoz páratlant (vagy fordítva) adunk vagy, ha páratlant veszünk el. Gyerekcsoportok „összevonásával”, „szétválasztásával” ez nagyon jól szemléltethető. (Például, ha az egyik padsorban páros számú gyerek ül, a másikban páratlan és a két csoportot összetereljük, a gyerekek megfigyelhetik, hogy a keletkezett új csoport páratlan létszámú lesz. Ha a páros létszámú osztályból kiválasztunk egy páratlan létszámú kisebb csoportot, vajon a helyükön maradók páros vagy páratlan létszámúak lesznek?

A 43. munkalap is megerősíti a fenti gondolatokat. Az egyforma számú ujjaimat, amit szimmetrikus mozgással mutatunk, összeadva páros számokat kapunk, és egyik felét elvéve (hátunk mögé dugva) ismét az egy kézzel mutatott számot kapjuk.

Amint változtatunk a szimmetrián, egyik kézzel eggyel többet mutatva, máris páratlan számot kapunk.

Később számolási eljárást is kapcsolunk ehhez a tevékenységhez. (Ha 7+7=14, akkor 7+8 eggyel több lesz.)

Kicsit szokatlan, de nagyon szemléletes, hogy a lábakon lévő ujjainkat is bevonjuk a számolásba. Az ötnél nagyobb számokat egy-egy oldalon tudjuk mutatni úgy, hogy a jobb láb 5 ujja és a jobb kéz 1 ujja jeleníti meg a 6-ot. „Összeszámoláskor viszont először a lábak 5-5-jét számoljuk, majd az 1-1 ujjat, mert így könnyebb.

44.munkalap: Ezeken a gyorsolvasási lapokon ellenőrizhetjük, hogy a gyerekek

felismerik-e a párosságot, felhasználják-e a szerzett matematikai tapasztalataikat. A képek számossága szándékosan húszon felüli. Azt akarjuk, hogy ne számlálgassanak, hanem ismerjék fel a kettesével kirakást, a tükörképet, az egyenlő csoportokat, a pároshoz páratlan hozzáadását. Ilyen feladatot megoldhatnak még a táblára, vagy írásvetítőre kirakott képen is. Rajzolhat ilyet a tanító sokat.

45 A és B munkalapok : a munkalapokon lévő „géppel „ is játszhatnak. Számokat dobok be a gépbe, a gép a párosokat és a páratlanokat különválogatja.

A gép rajzát sokszorosítjuk és a gyerek a számkártyáival kirakhatja, hogy ha bedobom az 5-öt, 7-et  8-at, a gép alul egyik nyíláson az 5-öt és a 7-et adja ki, a másikon a 8-at.

A gépeket egész évben használhatjuk. Kapcsolatok, kérdés-felelet játékok, szabályok, műveletek végzése, műveletek megfordítása, nyitott mondatok alkotása, mindezek gyakorolhatók vele.

Az egyszerűbb gépnek (45/A) egy bemenő nyílása van. A gép fordítva működik, ha megfordítom a lapot. A +-ból - lesz, a kisebbítésből nagyobbítás és így tovább. Például kis logikai lapot dobok be és a gép ugyanolyat, de nagyot ad ki. A szabály: a gép nagyobbít. Ha megfordítom a gépet, a nagy helyett kicsi jön ki, tehát a gép kisebbít.  A gép szabálya lehet még, hogy valamennyit bedobok, és valamennyivel több jön ki. De játszhatunk úgy is, hogy kevesebbet ad, mint amennyit bedobtunk. Sokfélét kitalálhat a tanító.

A másik gép két bemenő nyílású és egy kimenő nyílású (45/B). Ez a gép is megfordítható. Például bedobok 3 korongot az egyik és két korongot a másik nyíláson, lent 5 jön ki. Fordítva a gép a bedobott ötöt két számra bontja, a 3-ra és a 2-re.  De bedobhatok egy-egy színes rudat a nyílásokon, s a gép a kettő közül a rövidebbet dobja ki, azaz a kisebbet választja. Több eset megmutatása után a kisgyerek ráismer a szabályra.

Kép:Cikk 68 image009.jpg

Tematikus terv matematika 1.o.

Az alábbiakban egy első osztályos tantervhez kapcsolódó tematikus tervet olvashattok, amely a 10-es szám megismerésének épülését mutatja be. A 10 fontos szám, kimunkálására nagy hangsúlyt fektetünk. A téma februárban kerül feldolgozásra. A feladatok bármelyik másik szám bemutatására alkalmazhatók. A tematikus terv 5. órájának részletes leírását megtalálhatjátok az „óratervek” menüpontban. A tematikus terv formája, felépítése segíthet a portfóliótokhoz készülő tervek elkészítésében.

Tematikus terv

Műveltségi terület: matematika

Tantárgy: matematika

Évfolyam: 1. osztály

A tanulási-tanítási egység témája: A 10 vizsgálata

A tanulási-tanítási egység cél- és feladatrendszere: A 10 sokféle neve: számok előállítása sokféleképen. A 10 bontásai. „Szőnyegezések” leolvasása színekkel, számokkal. Számok „előállítása” sokféleképpen. Gyorsolvasási gyakorlatok. Állítások igazságtartalmának eldöntése. Szóbeli nyitott mondatok. Tájékozódás a számegyenesen. Számolási eljárások előkészítése. Számok írása, nagyságviszonyai. Grafikon leolvasása. Fejlesztési területek: emlékezet, megfigyelőképesség, szabályfelismerő képesség, összehasonlító képesség, összefüggés- felismerő képesség, problémamegoldó gondolkodás, számolási készség

A tanulási-tanítási egység helye az éves fejlesztési folyamatban, előzményei:

Előzmények:

17. hét A 9 valóságtartalma és egyszerű tulajdonságai. A 9 bontásai. Pótlás 9-re. Mondatok kiegészítése. Szöveges feladatok.

18. hét A 9 vázolása, írása. Növekvő és csökkenő számsorozatok. A változás jelölése. Gépjátékok. Pótlással megoldható feladatok. Tantárgyi kapcsolatok: olvasás, környezetismeret, erkölcstan

Felhasznált források: Útjelző - C.Neményi Eszter – Oravecz Márta /Nemzedékek Tudása/, Matematika munkafüzet 1. - C.Neményi Eszter-Oravecz Márta /Nemzedékek Tudása/, Matematika tankönyv 1.-C.Neményi Eszter-Oravecz Márta/Nemzedékek Tudása, Tantárgypedagógiai füzetek – Matematika (Kézirat)/Budapesti Tanítóképző Főiskola 1995. Interaktív tananyag: Matematika 1. osztály – Szilágyiné Oravecz Márta /Balázs-Diák Kft.

1. óra

Téma: a 10 vizsgálata: a 10 valóságtartalma és egyszerű tulajdonságai, számlálás

Fejlesztési területek: számérzet, megkülönböztetés és azonosítás, emlékezet, absztrahálás, tájékozódás papíron és füzetben

I. Beszélgetés tárgyakról frontális osztálymunkában

Eszközök: 10-es tojástartó, 10 elemből épített torony, 10-es csomagolású papírzsebkendő, 10-es csomagolású rágógumi, stb.

1.1 Szóbeli nyitott mondatok befejezése: állításokat fogalmazunk meg a tárgyakról, de a mondat vége nyitva marad. A gyerekeknek kell befejezni. Pl.: Van köztük… Nincs köztük… Mindegyikre igaz… Egyikre sem igaz…A szóbeli nyitott mondatok befejezése megalapozza a későbbi matematikai nyitott mondatok megoldását. Fejleszti a szókincset és a kifejezőképességet. Segít a fogalomalkotásban.

1.2 Állítások igazságtartalmának eldöntése: igaz-hamis játék a tárgyak tulajdonságai alapján. Ha igazat mondok a tárgyakról zöld, ha téves állítást mondok, piros ceruzát kell emelni.

1.3 Különbségek keresése: méretük, anyaguk, felhasználhatóságuk, csomagolásuk, stb.

1.4 Hasonlóságok keresése: méretük, anyaguk, felhasználhatóságuk, stb. A cél, hogy a gyerekek megtalálják, mindegyik tárgy kapcsolatban áll a tízzel

II. Tárgyak számlálása csoportban szervezett egyéni munkában

Eszközök: vászonzsák a csoportok száma szerint, minden zsákban: 10 elemből álló torony, 8 db gyufa összegumizva, 8 db gomb bezacskózva 8 db gyöngy felfűzve, 8 db színes pálcika összegumizva

2.1 Kakukktojás keresése: minden csoport kap egy vászonzsákot, melyben megszámlálandó tárgyak vannak. Mindenből ugyanannyit találnak a gyerekek, kivéve egy dologból, melyből 10 van, ez a kakukktojás, amit le kell rajzolni.

III. Több, kevesebb, ugyanannyi:

Eszközök: minden gyereknek 3 db postit lap, babszemek

2.1 Postit lapra ugyanannyi babszemet raknak, mint amennyi elemből állt a torony (10) az előző feladatban

2.2 Jobbra rakjanak a tíznél többet: a gyerekek megoldásai különbözőek lesznek. Érdemes megbeszélni, hogy miért.

2.3 Balra rakjanak tíznél kevesebbet: a gyerekek megoldásai itt is különbözőek lesznek. Érdemes megkeresni a legkisebb számot, ami igazzá teszi a relációt.

IV. Interaktív tananyag: Matematika 1. osztály – Szilágyiné Oravecz Márta /Balázs-Diák Kft. 4. fejezet: Hozzáadjuk, elvesszük

2. óra

Téma: Gyorsolvasási gyakorlatok. A 10 bontásai: bontás kétfelé, háromfelé

Fejlesztési területek: megfigyelő-képesség fejlesztése, figyelem és koncentráció fejlesztése, számolási készség fejlesztése

I. Gyorsolvasási gyakorlatok a tankönyvből frontális osztálymunkában

1.1 Képek megnevezése

1.2 Irányok, tájékozódás gyakorlása: Milyen tárgyat látsz a második sor, harmadik képén? A harmadik oszlop első képén? Lépj az első képről lefelé kettőt, azután jobbra hármat, azután balra egyet! Milyen tárgyat látsz? Stb.

1.3 Gyorsolvasás: Miből mennyit látsz a képen? Olvass a képről számtannyelven! A leolvasás tempója fokozható.

II. A 10 bontása kétfelé és háromfelé frontális osztálymunkában, párban és egyéni munkában Eszközök: 3 db hullahopp karika, minden gyereknek 2 db postit lap, babok

2.1 A tíz kétfelé bontott alakjainak leolvasása gyerekekről: 10 kisgyerek különböző módon áll be két hullahopp karikába

2.2 A tíz kétfelé bontott alakjainak leolvasása babszemekről: 10 babszemet szétosztanak a gyerekek két postit lapon. Párban dolgoznak, felváltva olvasnak a kirakásokról.

2.3 A tíz háromfelé bontott alakjainak leolvasása gyerekekről: 10 kisgyerek különböző módon áll be három hullahopp karikába.

2.4 A tíz háromfelé bontott alakjainak leolvasása babszemekről: 10 babszemet szétosztanak a gyerekek három postit lapon. Párban dolgoznak, felváltva olvasnak a kirakásokról.

III. Interaktív tananyag: Matematika 1. osztály – Szilágyiné Oravecz Márta /Balázs-Diák Kft. 3. fejezet: A számok bontott alakjai (1,2,3,8,9)

Megjegyzés: A bontásokat fokozatosan, fejből is megtanulják a gyerekek.

3. óra

Téma: A 10 vizsgálata: lépések a számegyenesen, a 10 szőnyegezése

Fejlesztési területek: megfigyelő-képesség fejlesztése, tájékozódás síkban, figyelem és koncentráció fejlesztése, emlékezet

I. Számegyenes használata frontális osztálymunkában

Eszközök: postit lapok

1.1. Számegyenes készítése postit lapokból a földön, lépésekkel mérve, 0-11-ig

1.2. Tájékozódás a számegyenesen: Hányat kell lépnem, hogy a 3-ról az 5-re érjek? Stb.

1.3 Számszomszédok leolvasása: Kik laknak a 8 mellett? Ki lakik a 4 és a 6 között? Stb.

II. Szőnyegezés rudakkal

2.1 A narancssárga rúd szőnyegezése

2.2 A bontott alakok leolvasása a kirakásokról. Lehet versenyt rendezni, ki tud adott idő alatt többet kirakni.

4. óra

Téma: A 0 és a 10 vázolása, írása

Fejlesztési területek: figyelem, koncentráció, formafelismerés, finommotorika, tájékozódás papíron, füzetben

I. A 0 és a 10 vázolása egyéni munkában

1.1 Vázolás morzsába: tálcára morzsát szórunk, amelybe a gyerekek ujjal vázolják a számokat a tanító bemutatása után. Jó tanács! Ha a morzsába levendulát szórtok, nem megy bele moly.

1.2 Vázolás 4 részre hajtott írólapra: négy egyenlő részre hajtva a lapot, nagyméretű téglalapokba vázolhatnak a gyerekek. A méretet fokozatosan csökkenthetjük további hajtogatásokkal.

1.3 Vázolás 8 részre hajtott írólapra

II. A 0 és a 10 írása négyzetrácsos füzetbe

III. Interaktív tananyag: Matematika 1. osztály– Szilágyiné Oravecz Márta /Balázs-Diák Kft. 3. fejezet: Megjegyzem a számok képét (1-9)

5. óra

Téma: A 10 vizsgálata: összegalakok és bontott alakok leolvasása

Fejlesztési területek: megfigyelő-képesség, számolási készség, szókincs, kifejezőképesség

I. Boltos játék frontális osztálymunkában

Eszközök: bolti áruk pl.: kekszes doboz, tejes doboz, pudingos tasak, sajtos dobozok, stb., játékórák

1.1 Az óra helyes leolvasása: a boltos játék mindig a nyitva tartás megbeszélésével kezdődik. Ez jó alkalom az óra leolvasásának gyakorlására. Játékórát használunk.

1.2 Ismerkedés a bolt termékeivel: megnevezzük a bolt termékeit, nevet adunk a boltnak. Tehetünk az árukészletbe kakukktojást, pl.: az élelmiszerek közé mosószert, vagy írószert.

1.3 Nyitott mondatok befejezése: állításokat fogalmazunk meg a bolt termékeiről, de a mondat vége nyitva marad. A gyerekeknek kell befejezni. Pl.: Van köztük… Nincs köztük… A szóbeli nyitott mondatok befejezése megalapozza a későbbi matematikai nyitott mondatok megoldását. Fejleszti a szókincset és a kifejezőképességet. Segít a fogalomalkotásban.

1.4 Igaz-hamis játék: ha igazat mondok a boltról zöld, ha téves állítást mondok, piros ceruzát kell emelni II. Összegalakok előállítása játékpénzzel

2.1 Összegalakok leolvasása, kirakása: a gyerekek szívesen játszanak játékpénzzel. Használjuk ki! Megadhatjuk a vásárolható tételek számát, pl.: 2 dolgot vehetsz! Vagy megadhatjuk a vásárlási keretet, pl.: Vásároljatok a boltban 10 petákból! Olvassák le az összegalakokat és bontott alakokat!

III. A 10 bontása

5.1 Játék az ujjakkal: párban játszható játék. Az egyik gyerek háttal áll a másiknak, aki 10 ujjából néhányat megfog, majd megkérdezi: Hány ujjadat fogom, és hányat nem fogok?

IV. Grafikon leolvasása: grafikon leolvasást szinte minden témában becsempészhetünk az órába. Szavazzanak a gyerekeket, hogy melyik feladat tetszet a legjobban. A szavazatukat leadhatják táblára ragasztott korong formájában, építőkockák, vagy dobozok egymásra rakásával, stb.

A laphoz nem tartoznak aloldalak.