Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Összefüggések, szöveges feladatok/Szöveges feladatok/A megoldás szakaszai/Modell alkozása/Modellezés számfeladattal, nyitott mondattal, függvényábrázolással

Az Alsós tanítói portálból

Szöveges feladat megoldása számfeladattal

3. osztály

 

Számfeladattal való megoldást akkor alkalmazunk, ha a feladat szövege azonnal sugallja a megoldást; ilyenkor esetleg az ábrázolás el is maradhat. Ez főképpen a már jól begyakorolt, nagyon egyszerű típusú feladatoknál fordul elő.

 

Például:

 

Egy zsákban 19 kg alma van. Mennyi van 10 ilyen zsákban? 11 zsákban? 9 zsákban? 20 zsákban?

 

Több van, hányszor több, szorzással oldható meg

19 kg ×10=

19 kg×10+ 19 kg=

19 kg×10-19 kg=

(19 kg×10) ×2

(A feladatot jól felhasználhatjuk a számolási eljárások gyakorlására.)

 

Szöveges feladatok megoldása nyitott mondattal

1. osztály

 

Erikának a cukorkás dobozában volt még néhány cukorkája. Megevett belőle ötöt és még maradt neki három darab. Rajzolj! Írd le a feladatot számtannyelven!

 

5 = 3

 

Az elvont nyitott mondatos leírásnál a gyereket segíti a dobozt jelképező keret felrajzolása.

 

 

2. osztály

 

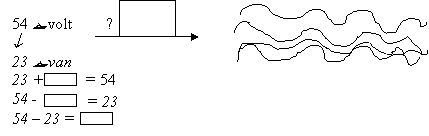
A kikötőben 23 hajó várakozik. Valamennyi már kifutott az 54 hajóból. Hány hajó vár még az indulásra? Rajzolj! Írd le a feladatot többféle nyitott mondattal!

 

                        

                     

Az ötletes és szemléletes rajzolás a megoldáshoz is elvezet. Lényeges, hogy a gyerekek tisztában legyenek azzal, hogy a „valamennyi” keresése a cél, amit többféle nyitott mondattal kereshetünk meg. Tudatosítsuk ezt az értelmező kiolvasáskor is:

- Valamennyi hajó már a vízen van, 23 a kikötőben. Együtt 54 van.

- Valamennyi hajó elment az 54 hajóból. 23 van most a kikötőben.

- Valamennyi hajó elment, amikor az 54-ből 23 maradt a kikötőben.

 

Törekedjünk arra, hogy a keresendő mennyiséget, a valamennyit mondjuk előre!

4. osztály

           

Nyitott mondatos modellhez akkor nyúlunk, ha a feladat szövegében rejlő összetett problémában az adatok kapcsolatait és összefüggéseit ábrázolni akarjuk, s egyben meg is akarjuk tervezni a megoldás lépéseit.

Az alábbi feladathoz ezt a modellt választjuk, de a feladatot egyben felhasználjuk a matematikai szövegértő képesség fejlesztésére is.

 

Május 29-től  június 2-ig tart az erdei iskola. A szállás ára személyenként 900 Ft/éjszaka, az étkezés 1200 Ft naponta. Mennyibe fog kerülni egy fő részére a táborozás, ha még 3200 Ft-ot a közlekedésre is ki kell fizetni?

 

A szöveges feladatok megoldásának egyik kulcsa, hogy a kisgyerek jól felismerje a problémákat, azaz jó kérdéseket tudjon alkotni.

- Vannak olyan kérdések, amelyekre a szöveg azonnal választ is ad. Ezeket a válaszokat azontúl vagy adatként kezeljük vagy feleslegesként elvetjük.

- Más kérdésekre a szöveg közvetlenül nem ad felvilágosítást, de maga a kérdés feltevése nélkül nem értelmezhető a probléma. Ezekre a kérdésekre a választ vagy rejtett összefüggés felismerése tárja fel, vagy külső információ segítségére van szükség.

Először is meg kell tanítani a kisgyereket a kérdésalkotásra.

 

Feladatlapon kapják a kérdéseket.

1. Húzd alá kékkel azt a kérdést, amelyikre a szövegben azonnal választ kapunk! Mettől meddig tart az erdei iskola? Máj. 29-től jún. 2-ig. Hányat alszunk? Hány ember költségét kell kiszámítani? Egy főét, „egy fő részére” írja a szöveg. Csak szállást és étkezést kell fizetni? „3200 Ft-ot közlekedésre is” Hány napot töltünk ott? Mit jelent az, hogy „900 Ft/éjszaka”?  kifejezés-magyarázatra van szükség Hány napos a május? Hány napos a június? Hányan fogunk táborozni?   2. Húzd alá pirossal azt a kérdést, amelyik szerinted még fontos a megoldás szempontjából!

 

 

Néhány gyerek ezalatt másik feladatlapon dolgozik.

 

Írj néhány olyan kérdést, amit fel kell tenni és meg kell válaszolni ahhoz, hogy a feladat megoldható legyen!

 

A megbeszélés során végigmegyünk a kérdéseken. Ahogy sorban megszületnek a válaszok, tisztázódik a kép, kibontakozik a matematikai probléma is. Először a közvetlen kérdésekre válaszolunk, majd sorra vesszük azokat is, amelyekhez külső segítségre van szükségünk.

Hány napos a május? A naptár vagy az öklünk segítségével kiderül, hogy 31 napos

Így már meg tudjuk mondani, hogy hány napot töltünk ott, azaz hány napra kell étkezést fizetni.

Hány éjszakát töltünk ott? Az előzőek alapján már könnyen kiszámolható, 4-et. 

Nem fontos a feladat szempontjából, azaz felesleges kérdés, hogy hányan leszünk, és hogy hány napig tart a június hónap.

 

Ezután megkérjük a gyerekeket, hogy egy nyitott mondattal írják fel a problémát. Majd mi is felírunk ötféle nyitott mondatot, s elemzésük közben a számokkal leírt problémát újrakonvertáljuk a szövegre.

900×4+1200 ×5+3200=□

900×5+1200 ×5+3200=♠

(900×4)+(1200 ×5)+3200=▼

(900+1200+3200)×5=◊

(900+1200)+3200×4=▲

 

Szöveges feladat ábrázolása függvénnyel

1. osztály

 

Ancsi és Robi kekszet ettek. Ketten összesen 6-ot. Mennyit ehettek külön-külön? Rakd ki!

   

     

ƒ
€

 

Adhatunk mi is egy üres táblázatot a gyerekeknek, amibe valóságos tevékenységgel, kirakással végzik el a 6 lehetséges bontásait. Koronggal, babbal, fehér kockákkal rakosgathatnak. Később ez az emlék segíti a táblázatok számokkal való ábrázolásában.

 

A	4	3	2	1
R	2	3	4	5

 

2. osztály

 

Katikának kétszerannyi szalvétája van, mint Évinek. Készíts táblázatot a gyűjteményükről!

           

K	15	26
É	30	52	84

 

3. osztály

 

Egy mókus és egy nyuszi indul egy helyről, egy irányba, egy időben. A mókus 5 m-es ugrásokkal halad, a nyuszi 10 méteresekkel. Hány ugrás után lesz a nyuszi előnye 60 m?

 

Az előkészítésben szövegelemzéssel kezdünk.

- Hány szereplő van?

- Honnan indulnak?

- Milyen irányba?

- Hogyan ugranak?

- Mekkorát ugrik a mókus?

- Mekkorát ugrik a nyúl?

Eljátszással folytatjuk a munkát. Két tanuló nyuszi és mókusfület köt a fejére, majd bemutatják az ugrásokat. Megfigyeltetjük, hogy nő-e közöttük a távolság vagy azonos marad. (Itt derülhet ki, hogy mennyire pontos képet alkottak a tanulók a szituációról, azaz egyszerre, egy irányba kezdik-e el az ugrásokat.)

Táblázatot veszünk fel:

Ugrások
Mókus
Nyuszi

Fontos kérdések:

- Az első ugráskor hány méterre lesz a mókus? Hány méterre ér a nyuszi?

- A második ugrásnál hogyan lesz?

- A harmadiknál?

- Folytasd a táblázat kitöltését!

- Keressük meg hol lesz a különbség!

- Figyeljük meg a számsorozatokat! Hogyan növekednek?

- Figyeljük meg a különbségsorozatot! Milyen szabályosság szerint növekszik!

- Hányadik helyen szerepel a 60 m-es különbség?

- Válaszoljunk a kérdésre!

 

Alkalmas a feladat a számegyenesen való lépegetéssel ábrázolásra is. Legyenek olyan gyerekek, akik ezzel az eljárással oldják meg a feladatot. Segítsünk! Elég nagy léptékű ötösével jelölt számegyenest adjunk. Hívjuk fel a gyerekek figyelmét, hogy kétféle színnel jelöljék az ugrásokat!

 

Megoldhatják nyitott mondattal is a feladatot. Kérjük, hogy utána magyarázzák el a gondolatmenetet.

 

Ez a két ugrás közötti különbség: 10 m-5m= „

Arra vagyunk kíváncsiak, hogy 60 m-be hány ilyen 5 m-es különbség fér. 60m:5m= 12

A laphoz nem tartoznak aloldalak.