Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Összefüggések, szöveges feladatok/Szöveges feladatok/A megoldás szakaszai/Modell alkozása/Szöveges feladat megoldása elvontabb ábrázolással
Az Alsós tanítói portálból
Tartalomjegyzék |
Ábrázolás diagrammal
2. osztály
|
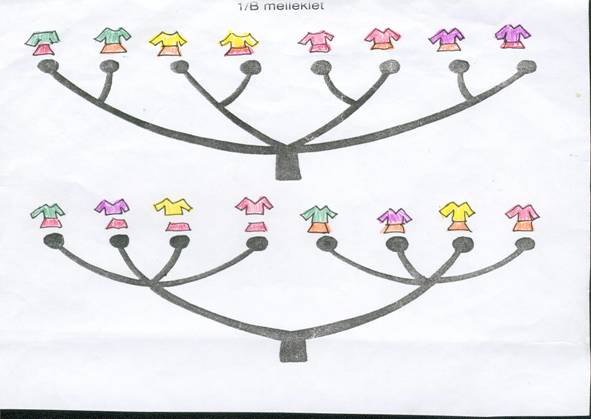
Zsuzsi babájának négyféle színes blúza és kétféle színes szoknyája van. Szeretné mindig másképpen felöltöztetni. Hányféleképpen tudja felöltöztetni a babáját? Rajzold le a „fa” segítségével az összeállításokat! |
A Venn-diagrammal való ábrázolással nem most találkoznak először a gyerekek. A logikai készlet egy-egy részét már rakosgatták a 6, 8, 12 ágú fákra.
A feladat megoldását igazán jól előkészíteni akkor tudjuk, ha a táblánál előre kivágott babaruhákkal próbálgatjuk a különböző összeállításokat.
- Tisztáznunk kell, hogy 6 féle színes ceruzára lesz szükségük a rajzolásnál.
- A gyerekek a rajzoláshoz kétféle 8 ágú fát kapnak.
- Az első fának négy nagy ága van, megbeszéljük, hogy arra kerülnek majd a blúzok, hisz négyféle színűek. Minden nagy ágból két kis ág nő ki, ezek fölé rajzolhatják a két-kétféle szoknyát.
- A másik fán két nagy ágból négy kis ág fölé rajzolnak úgy, hogy az azonos színű szoknyák és a négyféle színű blúzok látszanak egy-egy oldalon.
Le is írhatják számtannyelven:
Első fa: 2 · 4= 8
Második fa: 4 · 2= 8
Ez a szöveges feladat jól szolgálja a kombinatorikai témával kapcsolatos tennivalóinkat, de segít a szorzás műveletének egyik fontos tulajdonságáról, a felcserélhetőségről is tapasztalatot szerezni.
Területes ábrázolás
3. osztály
Ehhez a fajta modellalkotáshoz annak a gondolatnak az elfogadása szükséges, hogy egy adott terület képvisel egy mennyiséget, egy adott számot. A nála nagyobb terület nagyobb számot jelent, a kisebb kisebbet, a feleakkora pedig félannyit ér. Ha sokat foglalkoztunk a számfogalom alakításakor a számok megjelenítésével mind darab, mind mérőszám értelemben, akkor ez a gondolat nem idegen a gyerekektől. Gondoljunk csak akár a színes rudakkal folytatott munkára, akár a milliméterpapíron végzett leszámlálásokra, stb.
|
Délelőtt 295 személy volt a múzeumban, délután 180-nal többen mentek el. Hányan voltak délután? Hány ember járt a múzeumban aznap? |
- Megjelenítés kirakással
Ennél a feladatnál elővehetjük ismét a színes rudakat. A közelítő számlálásnál használt eljárásnak megfelelően egy világoskék rúddal megjelenítjük a délelőtt múzeumba látogató emberek számát. Egy világoskékkel (mert ennyien voltak délután is), és egy rózsaszín rúddal azokat, amennyivel többen mentek el délután.
- Megjelenítés területként
A rudakat letesszük a füzetre, és körberajzoljuk őket.
- adatok rögzítése rajzon (feliratozás)
A kapott területekbe beírjuk a szükséges adatot, s máris megjelenik a gyermek előtt a területes modell.
- adatok lejegyzése
|
|
De: 295 |
|
|
|
Du: 295+180 |
- feladatterv
Mindkét kérdésre választ tud adni, ha feladattervvé átfogalmazza a látványt
Egész nap: 295+(295+180)=?
(Persze ezt a feladatot a színes rúd segítségével szakaszos ábrává is át tudjuk dolgozni. Érdemes megtenni, mert így ugyanazon a feladaton sokféle modellalkotás válik lehetővé.)
Szakaszos ábrázolás
3. osztály
|
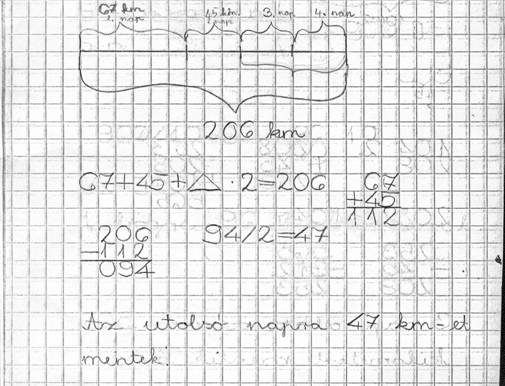
Apáék négy napos 206 km-es biciklitúrán vettek részt. Az első napon 67 km-t haladtak. Másnap 45 km-t tettek meg. A harmadik és a negyedik napon ugyanannyit kerekeztek. |
Egy harmadikos tanuló megoldásán nyomon követhető, hogyan gondolkodott a gyerek. Egy szakasznak fogja fel a 206 km-es utat. Jelöli rajta a két ismert hosszúságú első és második napi megtett utat. A maradék távolságot két egyenlő részre felosztja. Nyitott mondatában ugyanezt a gondolatmenetet Írja le: D × 2-ként írva le az utolsó két nap útját.
4. osztály
Két nyitott mondatot írtunk fel az órán. Először rajzon ábrázolták a gyerekek mindkettőt. A megbeszéléskor a két rajz közötti fő különbséget értelmeztük. Majd, hogy meggyőződjem arról, valóban értik-e, azt kértem, hogy írjanak szöveges feladatot is hozzájuk.
Lássuk a kész munkát!
A laphoz nem tartoznak aloldalak.