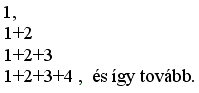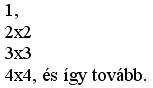Matematika/Hozzárendelhető segédletek/Tematikus tervezés
Az Alsós tanítói portálból
2007. december 9., 00:04 változat
Az alábbiakban egy első osztályos tantervi témának - számtulajdonságok vizsgálata témán belül a páros-páratlan fogalma - egyfajta feldolgozási lehetőségét mutatjuk be. A feldolgozáshoz munkalapokat mellékelünk. Ez a téma március, április táján kerül feldolgozásra.
Különböző számtulajdonságot vizsgálunk:
számok nagysága,
páros-páratlan fogalma,
számok kirakhatósága valahányasával, négyzetszámok, „lépcsős számok”, stb.
egyjegyű-kétjegyű számok,
számjegyek nagysága, alakulása műveletek elvégzése után
Tevékenységekkel, kirakásokkal, képolvasásokkal, rajzolással tehetjük szemléletessé a számtulajdonságokat. A tulajdonságok megtapasztalásakor egy-egy tulajdonsághoz hozzákeressük a rá jellemző számokat (a 20 körüli számkörben végzünk elsősorban megfigyeléseket). Most csak a páros-páratlan számtulajdonság feldolgozását emeljük ki.
A témához kapcsolódó feladatok
39.munkalap: Vágják ki a gyerekek a pénzeket és a négyzetlapokat. Ezek
hasznos eszközök, melyeket többször elővehetünk ennek a témakörnek a feldolgozása során. A pénzekkel, melyek lehetnek ‘Meseország” pénzei, kirakhatók a páros-páratlan számok, a 10-nél nagyobb számok, a csak 5-sel kirakható számok, stb. Vásárlásokat játszhatunk. A gyerekek ezekkel a pénzekkel fizetnek. (Lásd az 50. munkalap kirakata)
A pénzekkel játszhatják a gyerekek a „Kettes, ötös játékot”, persze ezt számkártyákkal is lehet játszani. Sok kettes és ötös kell hozzá. Próbálják kirakni a számokat kettesekkel és ötösökkel. A 10-et két ötössel (5+5) vagy öt kettessel (2+2+2+2+2) könnyedén kirakja a kisgyerek. A 11 és 13 kirakása már nem könnyű. Sok kisgyerek azt hiszi, hogy nem is lehetséges. Próbálkozzanak! Majd rájön, hogy 6+5 az 11, tehát három kettes és egy ötös kell. Vessük fel, vajon az összes szám kirakható? Előbb-utóbb rájönnek, ha az 5-2-t visszakérek, megkapom a 3-at. Ha 5-bõl két kettest kérek vissza, az egyhez jutok. Adjunk a kezükbe sok 5-ös és 2-es számkártyát, kivonás és összeadás jeleket és próbáljuk összegyűjteni 1-tõl húszig az eseteket.
A négyzetlapokkal jól megjeleníthetők a lépcsős számok (a matematikában háromszögszámként szerepelnek):
Megjeleníthetjük kirakással a négyzetszámokat is:
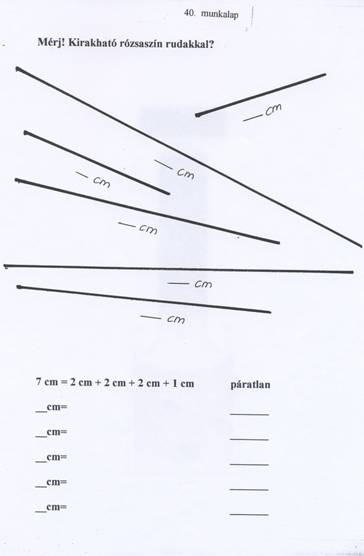
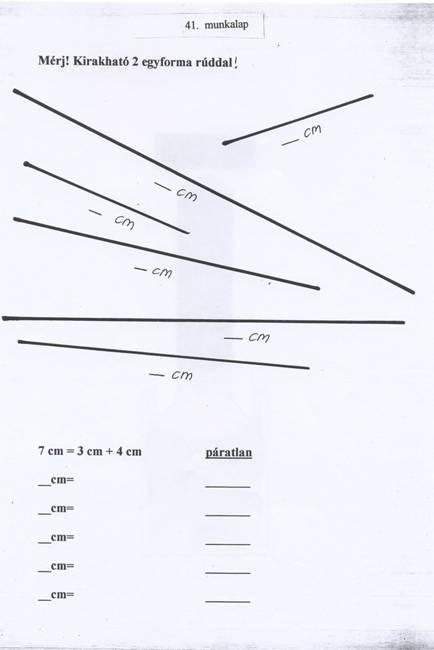
40-41. munkalap: A munkalapok használata előtt különböző számú gyerekcsoportok kialakításával vizsgálják meg, hogy tudnak-e párosával sorakozni vagy két egyenlő számú csoportot alakítani. 11 gyerek páratlan, mert sorakozáskor egy gyereknek nem jut pár. Azért is páratlan, mert a tornaversenyen az egyik csapatban eggyel több (vagy eggyel kevesebb) gyerek van.
A színes rudak közül a narancssárgát (a 10 cm-est) ki lehet rakni csupa 2 cm-es rózsaszín rúddal rakni, és két egyforma citromsárga rúddal (5-5 cm) is lemérhetem. A munkalapokon lévő vonalakat is e szerint vizsgálják.
42.munkalap: Korongokkal, fehér kockákkal, termésekkel, pénzérmékkel vizs-gálhatják a kettesével és a két egyforma csoportbavaló kirakást. Az átrajzolás és az írásbeli lejegyzés ugyanennek a tevékenységnek az absztraktabb megjelenése. Sok tapasztalatot nyújtsunk a kisgyereknek a páros- páratlan számtulajdonsággal kapcsolatban.
Szervezhetünk olyan tevékenységeket is, ahol a páros és páratlan számú darabokat tükörrel nézegetjük. A 3 gomb páratlan számú. Mellé téve a tükröt, 6 gombot látunk, ami páros szám lesz. A 8 gomb kétszerese 16 gomb lesz, a 8 páros tulajdonsága a kétszerezéskor is megmarad. Sok-sok tükrözés után jönnek rá a gyerekek, hogy tükörrel csak páros számokat tudnak előállítani.
Vizsgálják meg azt is, hogy mi történik, ha páros számhoz páratlant (vagy fordítva) adunk vagy, ha páratlant veszünk el. Gyerekcsoportok „összevonásával”, „szétválasztásával” ez nagyon jól szemléltethető. (Például, ha az egyik padsorban páros számú gyerek ül, a másikban páratlan és a két csoportot összetereljük, a gyerekek megfigyelhetik, hogy a keletkezett új csoport páratlan létszámú lesz. Ha a páros létszámú osztályból kiválasztunk egy páratlan létszámú kisebb csoportot, vajon a helyükön maradók páros vagy páratlan létszámúak lesznek?
A 43. munkalap is megerősíti a fenti gondolatokat. Az egyforma számú ujjaimat, amit szimmetrikus mozgással mutatunk, összeadva páros számokat kapunk, és egyik felét elvéve (hátunk mögé dugva) ismét az egy kézzel mutatott számot kapjuk.
Amint változtatunk a szimmetrián, egyik kézzel eggyel többet mutatva, máris páratlan számot kapunk.
Később számolási eljárást is kapcsolunk ehhez a tevékenységhez. (Ha 7+7=14, akkor 7+8 eggyel több lesz.)
Kicsit szokatlan, de nagyon szemléletes, hogy a lábakon lévő ujjainkat is bevonjuk a számolásba. Az ötnél nagyobb számokat egy-egy oldalon tudjuk mutatni úgy, hogy a jobb láb 5 ujja és a jobb kéz 1 ujja jeleníti meg a 6-ot. „Összeszámoláskor viszont először a lábak 5-5-jét számoljuk, majd az 1-1 ujjat, mert így könnyebb.
44.munkalap: Ezeken a gyorsolvasási lapokon ellenőrizhetjük, hogy a gyerekek
felismerik-e a párosságot, felhasználják-e a szerzett matematikai tapasztalataikat. A képek számossága szándékosan húszon felüli. Azt akarjuk, hogy ne számlálgassanak, hanem ismerjék fel a kettesével kirakást, a tükörképet, az egyenlő csoportokat, a pároshoz páratlan hozzáadását. Ilyen feladatot megoldhatnak még a táblára, vagy írásvetítőre kirakott képen is. Rajzolhat ilyet a tanító sokat.
45 A és B munkalapok : a munkalapokon lévő „géppel „ is játszhatnak. Számokat dobok be a gépbe, a gép a párosokat és a páratlanokat különválogatja.
A gép rajzát sokszorosítjuk és a gyerek a számkártyáival kirakhatja, hogy ha bedobom az 5-öt, 7-et 8-at, a gép alul egyik nyíláson az 5-öt és a 7-et adja ki, a másikon a 8-at.
A gépeket egész évben használhatjuk. Kapcsolatok, kérdés-felelet játékok, szabályok, műveletek végzése, műveletek megfordítása, nyitott mondatok alkotása, mindezek gyakorolhatók vele.
Az egyszerűbb gépnek (45/A) egy bemenő nyílása van. A gép fordítva működik, ha megfordítom a lapot. A +-ból - lesz, a kisebbítésből nagyobbítás és így tovább. Például kis logikai lapot dobok be és a gép ugyanolyat, de nagyot ad ki. A szabály: a gép nagyobbít. Ha megfordítom a gépet, a nagy helyett kicsi jön ki, tehát a gép kisebbít. A gép szabálya lehet még, hogy valamennyit bedobok, és valamennyivel több jön ki. De játszhatunk úgy is, hogy kevesebbet ad, mint amennyit bedobtunk. Sokfélét kitalálhat a tanító.
A másik gép két bemenő nyílású és egy kimenő nyílású (45/B). Ez a gép is megfordítható. Például bedobok 3 korongot az egyik és két korongot a másik nyíláson, lent 5 jön ki. Fordítva a gép a bedobott ötöt két számra bontja, a 3-ra és a 2-re. De bedobhatok egy-egy színes rudat a nyílásokon, s a gép a kettő közül a rövidebbet dobja ki, azaz a kisebbet választja. Több esetet megmutatása után a kisgyerek ráismer a szabályra.
A laphoz nem tartoznak aloldalak.