Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Műveletek/Műveleti sorrend
Az Alsós tanítói portálból
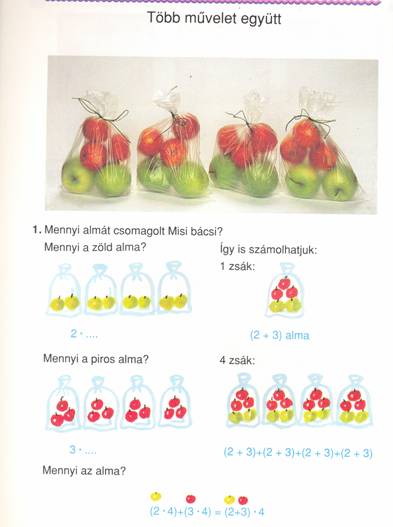
Kezdetben az összetett szöveges feladatokat többnyire két lépésben oldjuk meg. Második osztályban kezdünk el zárójeles feladatokkal foglalkozni. Akkor elsősorban az a fontos számunkra, hogy a kisgyerek az összetartozókat egy gondolataként, számalakban pedig egy számként lássa. A másodikos tankönyv II. kötete Több művelet együtt címmel dolgozza ki a témát. A bevezető kép rendkívül szemléletes: a nylonzacskókba csomagolt piros és zöld almák számát kell megállapítani. Színenként és zsákonként is számbavesszük az almákat. A leírás során akkor is kitesszük a zárójelet, amikor egyébként nem feltétlenül szükséges, hogy hangsúlyozzuk az összetartozást (szorzatalaknál). (Tankönyv 62-65. oldal)
<p A képolvasás után különféle hasonló kirakásokkal, történetek eljátszatásával segíthetjük az összetartozás megértését. Például 72 Ft-ból három ötforintost elvehetünk egyenként is, mindig elmondva, hogy éppen mennyinél tartunk, de elvehetjük egyszerre is 15 forintként. A második esetben inkább arra figyeltünk, mennyi fogy el összesen (ez kerül a zárójelbe), s így mennyi marad. Több olyan feladat után, amelyben a zárójel nélküli és zárójeles alakot is megvizsgáltuk, értik meg a gyerekek igazán a problémát. Tudatossá akkor válik bennük, ha ok maguk is képesek szöveget alkotni összetett zárójeles feladatokhoz. Harmadik osztályban ismét elokerül a téma (Tankönyv 41-42.). </p>
Harmadik osztályban ismét előkerül a téma (Tankönyv 41-42.).
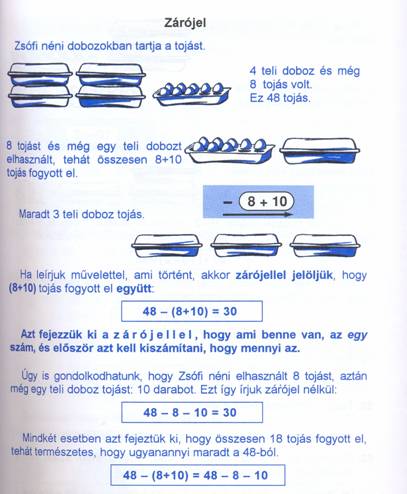
48 tojás egy részét elhasználjuk. 8 darabot és egy teli dobozt, melyben 10 darab tojás volt. Az elhasznált tojások mennyiségét egy összegalak fejezi ki: 8+10. Zárójellel jelöljük meg, hogy ez mind elfogyott. Eloször ezt az összeget kell kiszámítanunk. Ezt az összeget vesszük el a 48-ból.
Szükséges kimunkálni a gondolatot, hogy a zárójelben lévo érték egy szám valamely összeg-, különbség-, szorzat- vagy hányadosalakban felírva. Jól szolgálja a megértést, ha a zárójeles feladatok megoldásakor külön kártyára kerül a zárójelben lévo összeg-, különbség-, szorzat- vagy hányadosalak, s kiszámításkor a kártya hátára kerül a zárójelben lévo mennyiség eredménye egy szám alakban. A forgatásokkal erosödik a kapcsolat.
A zárójelhasználat gyakoroltatása történetalkotással történik. A történetek középpontjába a tartalmilag összetartozóknak kell kerülniük. A tartalmi összetartozás megértése nagyon fontos. Például a hét folyamán naponta egyenként elköltött zsebpénzt heti zsebpénz formájában fogjuk fel. Az egyenként elköltött 10 forintokat (10•7) hétszer tíz alakban egy számként: 70 forintként látjuk. Ezt a szemléletet alapozzuk hosszan elnyúló érési idot hagyva, közben érleljük a muveleti sorrend fogalmát.
A negyedik osztályban fontos feladatunk a muveleti sorrend tudatosítása. Az ötödik osztályba való továbbhaladás feltétele a helyes muveleti sorrend ismerete és alkalmazása. Két és fél éves folyamatot zárunk le a tudatosítással. Negyedik osztályban ez lehetové válik, már csak azért is, mert boséges tapasztalata gyult össze a kisgyereknek a muveletekkel kapcsolatban. El kell tudnia dönteni a kisgyereknek, hogy egy muveletsorban melyik muveletet kell eloször elvégeznie. A tankönyv a Zárójelek címu fejezetben alaposan kidolgozza ezt a témát, s majd késobb is az egész tanév során gyakoroljuk a tanultakat.
A muveleti sorrend megfigyeltetését a zárójelhasználathoz kapcsoljuk. Eloször olyan összetett szöveges feladatokat adunk a gyereknek, amelyeket megoldhat két lépésben is két muvelettel, de ösztönözzük, hogy egy nyitott mondatként fogalmazza meg a problémát. Vagyis ismét végigjárjuk az absztrakció útját.
Például:
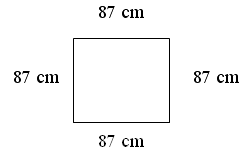
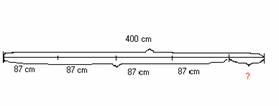
Klári 87 cm oldalú, négyzet alakú terítot akar beszegni. A szélére keskeny szegoszalagot vásárolt: 4 m hosszúságút. Hány centiméteres darab marad belole a munka elvégzése után?
A feladat előkészítéseképpen először becsléseket végeztetünk. Mekkora lehet a valóságban egy ilyen terítő? Mekkora asztalra való? Majd megmutatjuk a gyerekeknek egy valóságos terítőn a szegőszalagot. Felidézzük a négyzetről szerzett ismereteinket is.
Felírjuk, hogy a teríto kerülete egy
egyszeru szorzással kiszámítható.
Ha a kapott eredményt elvesszük a
4 m-bol, megtudjuk, hány centimé-
ter hosszú lesz a maradék szalag.
Számfeladatokkal két lépésben
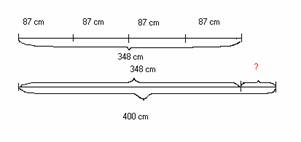
87 cm · 4 = 348 cm
4 m= 400 cm
400 cm – 348 cm = 52 cm
Ezután felírjuk együtt a feladatot egy nyitott mondatként is. Így gondolkodunk:
Ha az egész szalag hosszából
(4 m=400 cm) elvesszük a fel-használt szalag hosszát, megtudjuk milyen hosszú szalagdarab marad.
Nyitott mondattal:
400 cm - (87 cm X 4)=
A számfeladatokhoz és a szöveget pontosan tükröző nyitott mondathoz is szakaszos ábrázolást készítünk. Majd ezeket összehasonlítjuk.
Következo lépésként az eddig tanultak rendszerezéseként számbavesszük, hogy egy hosszabb muveletsort hogyan, milyen lépésekben, milyen sorrendben szoktunk megoldani. Eloször a zárójelben lévo muveletet, majd az osztást/szorzást, s legvégül az összeadást/kivonást oldjuk meg. A tankönyvben lévo elágazásos algoritmus nagy segítségünkre van a tanultak rögzítésében (Tankönyv 107/60). Elonye, hogy semmiféle felesleges elméletieskedést nem vezet be, s nem kényszeríti a gyermeket olyan verbális ismeretek befogadására, amelyeket még nem érthet meg.
E szerint az ábra szerint oldatjuk meg a kiszemelt feladatokat. Sok gyereknek az is segítséget jelent, ha a feladatmegoldás kezdete elott színes ceruzával jelzi, hogy milyen sorrendben fog haladni. Vagy beszámozással jelölheti a haladás menetét. Ez azért fontos segítség, mert a kisgyerek hajlamos elfeledkezni az elore megszabott sorrendrol, ha közben egy-egy hosszabb bíbelodést igénylo részletszámítás elvonja a figyelmét.
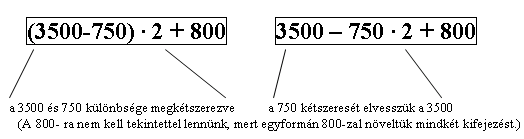
Nem akarjuk azonban, hogy átcsússzunk a lélektelen ismétlésekre szorítkozó unalmas feladatmegoldásba, ezért a muveleti sorrenddel kapcsolatos feladatokhoz is fontos megfigyelnivalókat kapcsolunk. Például két egymással majdnem egyforma muveletsort kell a kisgyereknek megfigyelnie, s számítás nélkül döntenie arról, hogy melyik értéke kisebb, nagyobb vagy éppen egyenlok:
Figyelje meg, s öntse szavakba, hogy a 3500 és 750 különbsége megkétszerezve nagyobb lesz, mint ha a 750 kétszeresét elvesszük a 3500-ból. A 800- ra nem kell tekintettel lennünk, mert egyformán 800-zal növeltük mindkettot! Nemcsak az a haszna az ilyen típusú feladatoknak, hogy tudatosítást végzünk, hogy az összetartozókat összetartozókként kezeljük, hanem az is, hogy a kisgyermek gyakorlatot szerez a muveletekben szereplo elnevezések használatában, s nem utolsósorban elokészítjük az algebrai kifejezések megoldásához szükséges stratégiákat.
Az e fajta feladatok alkalmasak arra is, hogy megfigyeltessük, nemcsak az eredményük különbözhet, de az a matematikai tartalom is, amelyet hordoznak.
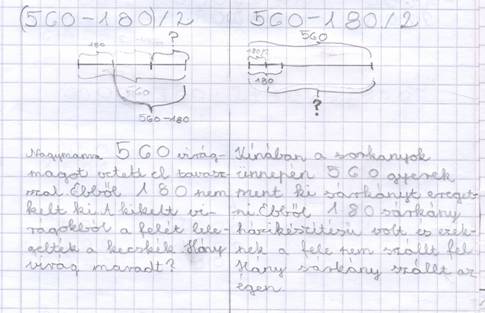
Az (560-180)/2 és 560-180/2 kifejezéseket eloször ábrázoltatjuk a gyerekekkel. Kétféle szakaszos ábrát fognak kapni. Mindkettot elemezzük rávilágítva a különbségekre. Majd ezután szöveges feladatot íratunk, mind a két ábrához. A megbeszélés során nemcsak matematikai tartalom szempontjából vizsgáljuk meg az elkészült szövegeket, hanem azt is ellenorizzük, hogy valóságos élethelyzetet jelenít-e meg a szöveg. Ha egy gyerek azt írja, hogy Peti 560 csokiból megevett 180-at, feltétlenül rá kell világítani ennek a valószerutlenségére. Ügyeljünk, hogy ez kello tapintattal történjék, nehogy a gyerekek megbántsák egymást.
Amint látjuk, a téma az absztrakciós út bejárásával és végül visszafelé történo bejárásával módszertani alapelveinknek megfeleloen kerül tanításra körülbelül januárban. A hátralévo idoben hosszú elmélyült gyakorlás következik. Mód van természetesen arra, hogy akik még nem értik, bizonytalanok, azok újra és újra végigjárják az absztrakció útját. Akár differenciált feladatszervezéssel, akár külön foglalkozással megtörténhet felzárkóztatásuk.
Lássunk egy tanulói feladatmegoldást!
Másik tanuló által alkotott szöveges feladat:
C. Neményi-Sz.Oravecz: Matematika tankönyv 2. osztályosok számára II.
C.Neményi-Wéber: Matematika tanköny 3. osztályosok számára
C. Neményi-Káldi: Matematika tankönyv 4. osztályosok számára
A laphoz nem tartoznak aloldalak.