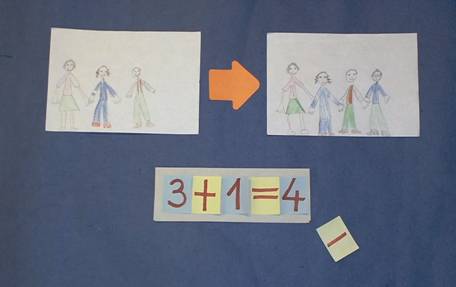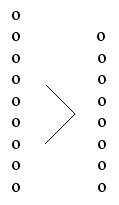Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Műveletek/Műveletek értelmezése
Az Alsós tanítói portálból
Az alsó tagozatban négy alapműveletet értelmezünk, az összeadást, kivonást, szorzást és az osztást.
Összeadás és kivonás
1. osztályban tanítjuk az összeadást és a kivonást mindig egymással párhuzamosan, hogy a műveletek közti összefüggésekről minél korábban tapasztalatokat szerezhessenek a gyerekek. Az összeadást, kivonást meg kell különböztetnünk az összeg- és különbségalakoktól. A gyerekek gyűjtik a számok sokféle nevét. Például a hatot 3+3 alakban vagy 10-4 alakban olvassák le. Nem a történet fontos, ahogy létrejött ez a kép, hanem maga a kép.
A műveletek értelmezését történetekhez kapcsoljuk. Eljátszunk, kirakunk, lerajzolunk történeteket, amiket aztán elmondunk „számtannyelven” is. (4 gyerek állt az asztal előtt. Ági néni kihívott még 2 kislányt. Hány gyerek van most kint? 4+2=6
Az összeadást, kivonást háromféle értelmezésben tanítjuk:
<p class=lista>Hozzáadás-elvételHalmazok egyesítése, részhalmaz elvétele
3. Összehasonlításon alapuló műveletértelmezés
Hozzáadás-elvétel
Mivel ez a legkönnyebb értelmezés, ezzel kezdjük a témakör tanítását. Ilyen cselekvések történések jellemezhetik az összeadást: odatettünk, kinyílott, odarepül, kapott hozzá, tett mellé, felgyújtott még, rakott a tányérjára, stb. A kivonást az eltörött, elrepült, elveszett, eldőlt, megevett belőle, stb. szavakkal érzékeltethetjük. A gyerekek el tudnak játszani olyan történeteket, amiben változást kell megjeleníteni. Ez lehet az a konkrét tevékenység, ami kiindulópontja az elvontabb, jelekkel kifejezett műveletek megtanításának.
Az eljátszásokat két képre lerajzolva lehet a legszemléletesebben megjeleníteni. A képek közé nyilat téve, a változásra hívjuk fel a figyelmet - kiment, leszállt, elveszett, bejött, felszállt, megtalált, stb.
Az itt látható gyermekmunkán jól látható, mennyire konkrét a megfigyelés: négy kisgyerek állt kint, egy kiment a folyosóra, hárman maradtak. A második képen ráismerhetünk a bentmaradó gyerekekre.
Hívjuk vissza a kisgyereket, akit kiküldtünk, s kérjük meg tanulóinkat, hogy ezt a történetet is mondják el számtannyelven. Majd jelöljük ki következő feladatnak azt, hogy e történetet is rajzolják meg két képben. Rögtön észreveszik, hogy felesleges újra rajzolniuk, mert elég a képeket megcserélniük!
A műveletek megfordításának elvont magyarázata helyett így válik érthetővé az összeadás és kivonás kapcsolata. A gyerekek azt is javasolni szokták, hogy a nyilat fordítsuk meg. Visszafelé már nem –, hanem + lesz a nyíl jelentése.
Már megrajzolt képekről is olvassanak a gyerekek, s mondják el a történeteket szavakkal és számtannyelven is.
Az absztrakciós utat a gyerekek visszafelé is járják be, adjunk olyan feladatokat is, ahol a művelethez kell a történetet rendelni.
Például: 6-2=4 Találj ki történetet a számtáblákról! Rajzold le két képben!
A korongos játék mint az értelmezéshez kapcsolható legérzékletesebb tevékenység
A tankönyv 61. oldalán található feladat sikeresen használható. Az Útjelző című kézikönyv használati útmutatót is tartalmaz.
Többször elővehető játék, később szavakkal is lehet rá utalni, ha az értelmezésre akarunk emlékeztetni. Később pénzzel is eljátsszuk ezt a tevékenységet, ahol a darabszámot a pénzre írt érték jelenti.
Mérőszámmal értelmezett tevékenységek
Eljátszásaink, kirakásaink között forduljanak elő mennyiségekkel végzett tevékenységek is.
Édesanya öt pohár vizet öntött a pörkölthöz, forrás után még hozzáöntött két pohárral. Hány pohár vizet használt a főzéshez?
Rakd ki korongokkal! Mondd el számtannyelven!
Fehérrel mérek. Toldd meg a sárga rudadat egy rózsaszínnel! Olvass róla számtannyelven! Vedd el a rózsaszínt! Így is olvass róla!
Lépj hármat. Lépj még kettőt! Hányat léptél?
Önts az üvegbe 6 pohár vizet! Meríts ki belőle 4 pohárral! Hány pohár víz maradt az üvegben? Próbáld ki! Mondd el számtannyelven!
Halmazok egyesítése, részhalmaz elvétele
Ebben az értelmezésben is a változást figyeljük meg, de itt a történés egyidőben zajlik. A kezemben 3 ceruzát és 2 filctollat tartok. Matematikailag az történik, hogy a ceruzák és filctollak halmazát egyesítjük. Művelettel: 3+2 ugyanannyi, mint 5. Ha az írószerek halmaz egy részéről akarunk beszélni, például a ceruzákról, azt a kettőt veszem el, amelyik nem ceruza, ezért fölösleges. 5-2 a ceruzák száma.
A lejegyzés összeg- és különbségalakban jelenik meg és a művelet elvégzése, azt jelenti, hogy az eredményt egy szám alakban is megmondjuk. 5-2 ceruzám, azaz 3 ceruzám van.
A gyerekek körében nem használjuk sem a halmaz, részhalmaz, sem az egyesítés szavakat, mert ezeket az elnevezéseket, nem értenék. Mennyi az összes? Mennyi egy része?– mondjuk helyettük.
Ez az értelmezés is eljátszásokhoz, kirakásokhoz kapcsolódjon.
Közös eljátszással találkozhatnak először ezzel az értelmezéssel a gyerekek.
- Ez a 3 fiú és ez a 2 lány, ha tapsolok, jöjjön ki!
- Mi történt?
- Mondd el a történetet!
- Mondd el számtannyelven is! /3+2/
- Azt is mondd el, hány gyerek van itt! /5/
Az egész történetet elmondjuk számtannyelven és lejegyezzük. /3+2=5/
Ezzel az egyesítést jelenítettük meg.
A részhalmaz kifejezése nehezebb, de jól segítheti a megértést a letakarás. Hány fiú van itt? /Természetesen rávágják a gyerekek, hogy 3!/ A két lányt ekkor letakarom egy lepedővel.
- Az összes gyerekből hányat takartam el?
- Mondd el számtannyelven! /5-2/
- Mondd el azt is hány fiú látható! /5-2=3/
A kirakásoknál üres gyufásdobozzal, lappal, ronggyal takarhatnak a gyerekek. Ha átlátszó anyaggal végzik a takarást, még könnyebb a leolvasás, mert jól látja a kisgyerek, hogy mennyit kell elvenni az összesből.
Adhatunk a gyerekeknek például 3 kukoricát, 2 babot. Átlátszó műanyagdobozzal vagy mással letakarjuk. Az írásvetítőn mi is elvégezzük a kirakást.
Mennyi az összes? 3+2=5 vagy 2+3=5
Mennyi a bab? 5-3=2
Mennyi a kukorica? 5-2=3
Mindig a fölösleges, - amely nem rendelkezik az adott tulajdonsággal, azaz nem való a halmazba, - kerül letakarásra. Ami kukorica, az nem bab. A letakarásra, addig van szükség, amíg a kisgyerek el nem sajátítja a szükséges látásmódot.
Természetesen többféle tárgy, dolog kerülhet egy halmazba /dobozba, zacskóba, akváriumba, tányérra, stb.!/, nemcsak kétféle. Arra ügyeljünk, hogy legyen mindig olyan közös tulajdonság, ami összeköti őket.
A babos játék mint az értelmezéshez kapcsolható legérzékletesebb tevékenység
Az összeadás felcserélhetősége /a+b=c; b+a=c/, az összeadás, kivonás kapcsolata /a+b= c; c-a=b; c-b=a / mozgásos tárgyi tevékenységgel jól érzékeltethető, ha sokszor alkalmat adunk az eljátszására.
Vegyenek az egyik kezükbe is és a másikba is valamennyi babszemet. Egymáshoz közelítve a nyitott tenyerükön lévő babszemekről olvassanak számtannyelven: 2+4=6 A kislány balról jobbra olvassa le, amit a tenyerében lát.
Cseréljék meg a kezüket, és így is olvassanak a babokról: 4+2=6
Dugják hátra az egyik kezüket, és olvassák le az elvételt. Állapítsák meg azt is, hány babszem maradt látható: 6-2=4
A másik kezükkel is játsszák el az eldugást és végezzék el a leolvasást: 6-4=2
Ez a tevékenység később segíti a műveletértelmezés felidézését, felújítását a számfeladatok megoldását, az összes pótlásos feladat megértését nagyobb számkörben is.
Még a helyi érték mélyebb megértésében is szolgálatunkra lehet: az egyik kezébe a tízeseket teszi, a másikba az egyeseket.
Mérőszámmal értelmezett tevékenységek
Jól szemlélteti az egyesítéseket, részhalmazok elvételét a kétkarú mérlegen való tömegmérések alkalmi egységekkel.
Színes rudakkal játszhatják a gyerekek: Két rúd együtt ugyanolyan hosszú, mint a narancssárga. Keressenek ilyen rudakat! Olvassanak róluk! Párban folytathatják: Az egyik gyerek egy rudat ad a másiknak a maga párjából. Õ kitalálja, mit tartott meg magának a társa. Például: a rózsaszín rúd és a bordó rúd együtt ugyanolyan hosszú, mint a narancsszínű. Ha a társnak megmutatja a rózsaszínű rudat, akkor a másiknál csak is a bordó lehet.
Összeadás, kivonás összehasonlítás alapján
Az összeadás, kivonás összehasonlítás alapján műveletértelmezés a gyermek számára a Mennyivel több? Mennyivel kevesebb kérdésekre való válaszadás közben tisztázódik. Sokak szerint ez a legnehezebb értelmezés. Nagyon sokféle tevékenységet végezzünk. A témát alaposan elő kell készítenünk, mielőtt kifejeznénk számtannyelven is magunkat. Sokféle összehasonlításra adjunk lehetőséget a magasabb-alacsonyabb, hosszabb-rövidebb, több vagy kevesebb fér bele, rövidebb ideig tart-hosszabb ideig tart, stb. relációk körében. Hasonlítsanak össze építményeket, edényeket, madzagokat, gyöngysorokat, stb.
Érdemes konkrét játékhoz kapcsolni akkor az értelmezést, amikor már művelettel is ki akarjuk fejezni az összehasonlítást. Két csapathoz hívunk ki gyerekeket. Szándékosan úgy, hogy az egyik csapatban eggyel többen legyenek.
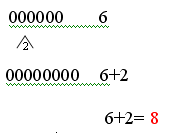
Hasonlítsuk össze a csapatokat! Versenyezni szeretnének. Mit tehetünk, hogy igazságos legyen a játék? Vagy hívok még egy gyereket oda, ahol kevesebben vannak vagy helyreküldök egy gyereket onnan, ahol többen vannak. Mind a két esetben elmondjuk a történetet számtannyelven: Például 8 és 9 gyerek esetében: 8+1=9 vagy 9-1= 8
Ugyanezt a történetet kirakjuk korongokkal is. Közéjük tesszük az összehasonlítás jól ismert jelét, s bele is írjuk az összehasonlítás eredményét.
Elmondják a gyerekek számtannyelven, hogy mi történt, mikor kihívtunk még egy kis gyereket: 8+1= 9
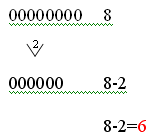
Amikor helyére küldtünk egy tanulót, akkor: 9-1=8
A Lego-tornyok összehasonlításához köthetjük az értelmezést. Ez lehet az a konkrét tevékenység, aminek képi felidézése segíti a fogalom kialakulását Jól ismert játék, könnyen lerajzolható, leszámlálható. Jól látszik a magasságbeli különbség. Ekkor már fordítsunk gondot a lejegyzésre is.
Ha feladattá formáljuk a kirakást, akkor a kérdés dönti el a számfeladat felírását.
Nóri 6 cukrot rakott sorba. Ancsi cukorsora két darabbal hosszabb.
Hány cukra van Ancsinak?
Ancsi 8 cukrot állított sorba maga elé.
Ancsi 8 cukrot állított sorba maga elé. Nóri cukorsorához kettővel kevesebb kellett.
Hány cukra van Nórinak?
Nórinak 6 cukra van.
Adódhat még egy kérdésünk a feladat kapcsán: Mennyivel több (kevesebb) az egyik cukorsor a másiknál- ez a kivonásnak egy negyedik értelmezése, mely a számok különbségére irányul, ami annyira szorosan kapcsolódik a fentiekhez, hogy külön nem kap helyet a műveletek tanításában, de a kirakások, szöveges feladatok ilyen tartalommal is megjelennek./
A kirakás, rajzolás soha ne maradjon el! Csak az a kisgyerek lesz képes egy-egy fordított szövegezésű feladat helyes megoldására, aki az értelmezéshez a kirakást vagy rajzolást segítségül tudja hívni.
Mérőszámmal értelmezett tevékenységek
Ennél az értelmezésnél az esetek többségében mérőszámokkal dolgozunk. Megint hasznos eszközünk lehet a színes rúd, amivel a hosszúság, terület, térfogat /felfelé építések/ területén tapasztalhatunk. A tömegmérés eszköze lehet a fogasmérleg, a súlyok helyett érméket, üveggolyókat használhatunk.
Második osztályban új műveletekkel bővülnek az ismereteink, a szorzást, osztást is értelmezzük.
A szorzás
A szorzás egyszerűbb, s a tapasztalatszerző munka során leggyakrabban előforduló értelmezése az egyenlő számok összeadásán alapul. Már az első osztályban is többször találkoztak a gyerekek olyan estekkel, amikor egyenlő számokat kellett összeadniuk. Már akkor fellépett néhány kisgyerekben az igény az egyszerűbb kifejezésmódra. 2+2+2+2+2+2+2=14, a kettőt hétszer írtuk le. A szorzást az ilyen jellegű összeadások gyakorlásával készítjük elő. Természetesen a valahányasával való számlálás is része ennek a gyakorlásnak, hisz ezzel a szorzási esetek megjegyzését is megalapozzuk.
Adhatunk mignon tálcákat a gyereknek, ezek használata segíti azokat a kirakásokat, amikben valamilyen étel szétosztása szerepel a történetben.
Anyu, apu, és a három gyerek lekváros gombócot kaptak ebédre. Mindenkinek három gombócot tett anyu a tányérjára.
Egészen addig lehet késleltetni a szorzás írásbeli kifejezését, amíg nem rögzül a kisgyerekekben a helyes leolvasás.
(A szorzás egy másik értelmezéséről, a halmazok direktszorzatáról bővebben most nem beszélünk, hisz ez az értelmezés inkább a kombinatorikai feladatokhoz kapcsolható. Csak példaképpen említjük: a kétféle nadrágból és ötféle blúzból 2x5 vagy 5x2-féleképpen állíthatjuk össze az öltözetünket, s ebben a szorzásban nem szorzandóról és szorzóról, hanem tényezőkről van szó.)
Az osztás
Szakmai vitákban sokszor vetődik fel a kérdés, beszélhetünk-e kétféle osztásról. Ha komolyan vesszük azt a módszertani elvet, hogy a kisgyerekeknek csak a valóságból merített konkrét cselekvésekkel tudunk kellő tapasztalatot nyújtani a tanulás során, akkor be kell látnunk, hogy az osztás megértéséhez szükséges a kétféle értelmezés.
A tízben a kettő (10:2) és a tíz osztva kettővel (10/2) osztás eredménye számszerűen megegyezik, ez a szorzás kommutativitásából ered, mégis más-más tevékenység által jön létre.
Konkrét példán érzékelve:
Az „Apu 10 szelet nápolyit hozott haza. Mindenkinek 2 szeletet tudott adni, hányan vannak a családban? -szövegű feladat azt a tevékenységet kelti életre, amikor a kisgyerek a 10 pálcikát kirakva kettesével csoportosít, s megállapítja, hogy a tízben a kettő 5-ször van meg.
A feladat adatai és kérdése erre a műveletre vezetnek: 10:2=5 (10 nápolyiban a 2 nápolyi 5-ször van meg). Ez a művelet a bennfoglalás.
Az „Apu 10 nápolyit hozott haza. A két gyereke között igazságosan szétosztotta. Hány szelet nápolyi jutott egy gyereknek?” -szövegű feladat pedig egy másik tevékenységet kíván. A gyerekek elkezdik „egy ide- egy oda” módszerrel kétfelé osztani a pálcikákat, s megállapítják, hogy mind a két gyerek 5- 5 nápolyit kapott.
A feladat adatai és kérdése erre a műveletre vezetnek: 10/2=5 (10 osztva kétfelé vagy 10-nek a kettede az 5). Ez a művelet a részekre osztás.
A bennfoglalás megértését követően állítsuk olyan helyzetek elé a gyerekeket, amikor a valahányasával szétosztás során az utolsó mignon tálcára vagy zacskóba nem jut annyi sütemény, alma, ahányasával szét akarták osztani. Ezzel a maradékos osztás fogalmát tudjuk előkészíteni. A maradékos osztás jól értelmezhető a szorzás segítségével is: 11-ben a kettő megvan 2-szer és marad egy, mert 2-szer 5 az tíz, 10+1= 11 Röviden: 5·2+1=11
A lejegyzés a korai szakaszban nem lényeges, ráérünk ezzel majd a szorzó és bennfoglaló táblák felépítése után is.
A maradékos osztás egy-egy esete a bennfoglalással értelmezett osztásnak, ezért nem értelmezzük új műveletként.
Szorzótáblák és bennfoglalótáblák tanítása
A másodikos tankönyvcsaládban a szerzők egy külön fejezetben foglalkoznak a szorzás, osztás, bennfoglalás „egyszerű eseteivel”, hogy a százas számkör feldolgozása alatt szerzett tapasztalatokra építve még jobban előkészíthessék a tanulókat az új műveletek megértésére.
Lényeges, hogy milyen sorrendben tanítjuk a szorzó és –bennfoglalótáblákat, mert csak így nyílik lehetőségünk a táblákon belüli és a táblák közötti összefüggések feltárására és a műveleti tulajdonságok megismerésére. A tankönyv ezt a sorrendet követi: 2, 5, 10-es; 4-es; 8-as; 3-as; 6-os; 9-es; 7-es szorzó és –bennfoglalótáblák.
A bennfoglalás írásbeli kifejezésére csak később kerül sor, amikor már a megértés biztosított. A részekre osztás a legnehezebb a műveletek között, ezért ennek a tanítása is későbbre esik. A 2-es, 5-ös, 10-es táblák feldolgozása közben tanítjuk a jelölt bennfoglalást, a 4-es szorzó- és bennfoglalótáblák után a részekre osztást. (Tk. II. kötet 26-27. oldal)
A laphoz nem tartoznak aloldalak.