Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Számfogalom - a számfogalom tapasztalati alapjai/Negatív számok
Az Alsós tanítói portálból
Tartalomjegyzék |
Negatív számok 3-4. osztályban
A számfogalom építésének témakörébe tartozik a negatív számokkal való ismerkedés is. Csak konkrét tapasztalati értelmezés, illetve értelmezést mélyítő egyszerű műveletek végzése " kiegyenlítés " a feladatunk. Az értelmezés alapja az iránnyal való negatív szám képzet kialakítása "számegyenesen 0-tól balra, hőmérőn lefelé "illetve hiányként való felfogás. Mindkét tapasztalati alapon el kell jutni a negatív számok sokféle nevéhez, ezeket tevékenységgel, rajzzal elő kell állítani. Ez lesz az alapja a felső tagozaton a műveletvégzésnek.
Követelmény csak annyiban fűződik a témához, hogy tudjon a kisgyerek leolvasni hőmérőről negatív hőmérsékletet. Tudjon adósságból és készpénzből álló vagyont leolvasni. Majd negyedik osztályban továbblépünk az önálló megjelenítés felé.
Mindenképpen meg kell különböztetnünk a negatív számot a kivonástól, ezért jelölésében a mínuszjelet kissé feljebb írjuk a szám elé, mint a műveleti jelet szokás.
Negatív számok a hőmérőn
Hőmérőmodellen (függőleges helyzetű számegyenes.) kezdjük az ismerkedést a negatív számokkal. Téli időszakban tanítjuk a témát, amikor a rádió, televízió és az újságok időjárás jelentéseiben sűrűn előfordulnak negatív hőmérsékletek jelzőszámai. Ekkortájt ismerkedünk a fagyás-olvadás témával. A 0 Celsius fok kitűntetett szerepe érthető a gyerekek számára, mert megfigyeléseik közben tapasztalják, hogy a fagyás-olvadás 0°C-on következik be. A megértéshez szükséges a hőmérő működési elvének tisztázása: az üvegcsőben lévő anyag meleg hatására kitágul, hideg hatására összehúzódik. Hozzárendelünk egy skálát, a viszonyítási pont a víz fagyás- illetve olvadáspontja. (A tantárgyak közötti koncentrációnak nagy szerepet szánunk. Ezeket az ismereteket a környezetismeret tantárgy keretében szereztük. Sokféle mérési gyakorlattal biztosítottuk a szükséges mennyiségű tapasztalatot, így bízvást számíthatunk arra, hogy a gyerekeknek ez nem okoz problémát.)
Hasznos a mozgatható hőmérő modell használata (ebből van tanári demonstrációs és tanulói példány is). Ha nincs, kartonpapírból könnyen előállítható. Jó, ha a gyerek látja, hogy az üvegcsőben lévő folyadék magasabb oszlopban áll, ha melegebb van, és az oszlop alacsonyabb, ha hidegebb van. A hőmérő modellen beállítjuk az adott hőmérsékletet a pirosra színezett gumiszalag mozgatásával. A különböző hőmérsékleteket rajzokon is úgy ábrázoltatjuk, hogy az egész oszlopot színeztetjük, s nem csak az adott pontot jelöltetjük meg. (Munkafüzet 52/1. feladat)
Feladataink:
leolvasások
hűlés, melegedés közben a hőmérő higanyszála elmozdulásának megfigyelése
változások előállítása hőmérőn.
Ehhez azt kell értenie a gyermeknek, hogy hőmérséklet-változás lehűlés vagy felmelegedés következtében állhat be (Munkafüzet 52/1 és 2. feladatok). Amikor arról beszélünk, hogy 10 fokról 0 fokra változott a hőmérséklet, a levegő felmelegedett, mégpedig 10 foknyit. A hőmérő higanyszála ilyenkor felfelé mozdul. 2 fokból lehűlés következtében lesz 0 fok. Ne mondjuk, hogy hűlt 2 fokot, mert a hűlés maga a változás irányát adja meg. Így a jelentése éppen ellenkező lenne, azt jelentené melegedett 2 fokot. Ügyeljünk arra, hogy nagyon pontosan fogalmazzunk a kisgyereknek.
Függőleges irányú lépegetések
Sokat segíthet a gyerekeknek a földszinthez való igazodás. Könnyen megértik, hogy ehhez képest a lefelé történő haladás a pincébe az első emelet, a földszinthez képest való felfelé haladás az első, második vagy harmadik szintre jutás. Sokat segít az is, hogy a liftek kijelzői használják a 0 jelölést a földszint jelölésére, a negatív számot az alagsor vagy pince jelölésére.
Negatív számok a számegyenesen
A 0-hoz viszonyított jobb-bal irányú lépkedésekkel építjük a negatív szám fogalmát. Segítségül először a hőmérőskálát vízszintes helyzetbe hozzuk. Majd vízszintes irányú lépkedéssel folytatjuk a munkát. A számegyenesen való lépkedések nagyon sokat segítenek a gyermeknek a negatív és pozitív számok közt való tájékozódásban.
Térbeli mozgásokkal készítjük elő. Először jobbra-balra lépésekkel, vagy előre hátra mozgással, esetleg lépcsőn lefelé és felfelé lépegetéssel.
Két színes kockával dobunk, megállapodunk, hogy az egyik szín a balra, a másik a jobbra, az egyik a le, a másik a felfelé lépést, az egyik a negatív, a másik a pozitív számot jelenti. Egyszerre dobunk, s leolvastatjuk a kockákról a dobott értékeket. Majd lelépkedjük. Megfigyeltetjük a tényleges haladást is. Nagyon szeretik ezt a játékot, mert a mozgással való tanulás, még a leggyengébb képességű gyereknek is sikerélményt hoz. A dobókockával való játékok haszna, hogy biztosítják a kis számkört. Megerősítik a gyerekek balra és jobbra mozgásként való felfogását, sőt lehetőséget adnak olyan megfigyelésekre is, amelyekkel már a műveletvégzéseket készítjük elő. Természetesen semmiképpen sem akarunk műveleteket tanítani, mert ez nem a negyedik osztály feladata, de óhatatlanul megfigyelik a gyerekek, hogy ha + 5-öt és -3-at kell lépnie egymás után, akkor a tényleges elmozdulás + 2.
Ha már sokat mozogtunk, játsszunk a számegyenesen is! Lehet bábuval vagy ceruzával lépegetni
Adósság-vagyon
A hiány oldaláról is megközelítjük a negatív szám fogalmát. A hiányt könnyen megérti a gyerek, ha konkrét helyzethez kapcsoljuk: többen vagyunk a teremben, mint ahány szék van. Hozni kell még, hogy mind le tudjunk ülni. Van, amikor vagyonom van, máskor csak adósságom. Ha a vagyonom és adósságom mennyiségét számba veszem, adósságaimat kiegyenlítem, lehetővé válik a vagyoni helyzetem megállapítása.
Kirakások:
Történetet mesélünk a gyerekeknek. Próbálják meg kirakással követni. A kölcsönkért pénz megjelenítésére javasoljuk, hogy írjunk adósságcédulát. Ollóval kivágjuk, s ráírjuk 1 Ft. Hogy megkülönböztessük a meglévő forintjainktól, négyzet alakúakat vágunk. Ezután már menni fog a kirakosgatás. Később a logikai készlet körlapjaival jeleníthetjük meg az 1 forintnyi vagyont, négyzetlappal pedig az 1 Ft adósságot reprezentáljuk.
Vagyon számbavétele
Ezek vannak a pénztárcámban:
1 Ft adósságom van, ezt kiegyenlítem 1 Ft készpénzzel. Tehát 2 forintom van.
Fontos az adósság megadását eljátszatni. Az adósságcédulára tesszük a Ft-ot, mutatva, hogy ezt a tartozást most kiegyenlítettük.
Pénztárcákat alakítunk ki. Ezekbe kevés adóság és vagyon cédulát rakunk. Állapítsa meg a kisgyerek, mennyi a vagyonunk. Kezdetben a kirakásokat, kiegyenlítéseket, leolvasásokat közösen végezzük.
Láncszámolások: Történetet kerekítünk a vagyon változásaihoz. A gyerek kirakásokkal követi a történetet, majd a végén számba veszi a vagyont.
A számok sokféle neve, a negatív szám sokféle neve:
Észrevetetjük a gyerekekkel, hogy 2 Ft-ot sokféleképpen is kirakhatnak.
-3 Ft is sokféleképpen előállítható. Bátorítjuk őket, hogy minél találékonyabbak legyenek a kirakásban. Minden gyerek a saját absztrakciós képessége szintjén fogja hozni a megoldásokat. Lesznek, akik csak az egyesek körében fognak gondolkodni, mások kimerészkednek a 20-as, 30-as számkörbe is.
A negatív számok nagysága
A negatív és pozitív számok nagyságviszonyait hőmérséklet alapján értelmezve úgy fogalmazzuk meg, hogy két adat közül az a nagyobb, amelyik melegebbet fejez ki. Megfigyeltetjük külön pozitív értékek összehasonlításával, majd pozitív és negatív hőmérsékleteket hasonlítunk össze. Végül negatív és negatív értékek közül is kiválasztjuk a nagyobbat. "Melyik jelent melegebbet?" kérdéssel segítünk a gyerekeknek. Lássunk egy órarészletet!
Tudod-e, hogyan működik a hőmérő?
Mit jelent a 0 ˚C? (A víz fagyás és olvadáspontja)
Merre mozog a hőmérő higanyszála, ha 0 foknál melegebb van?
Merre mozdul, ha 0 foknál hidegebb van?
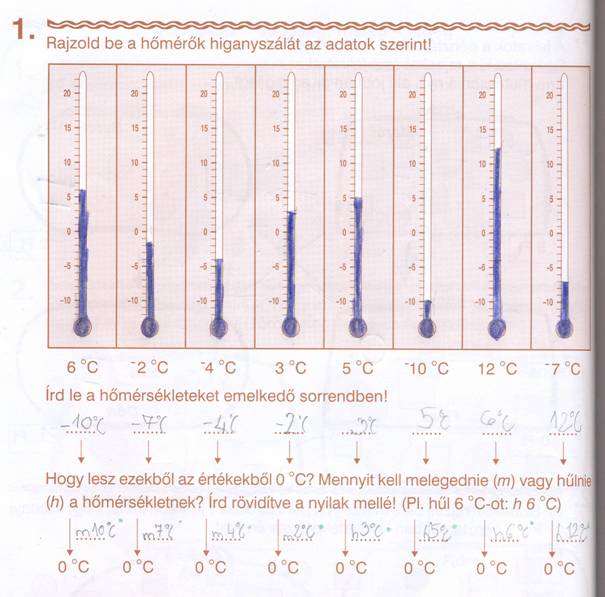
Munkafüzet 52/1. Csak a higanyszál állását rajzold be! Színezd ki, meddig van a higany az üvegcsőben!
Azt kéri tőlünk a munkafüzet, hogy írjuk nagyság szerint le a hőmérsékleteket. Ehhez össze kell hasonlítani.
Melyik érték jelenti a melegebbet? Melyik a hidegebbet?
A nagyobb érték melegebbet jelent. Mondj rá példát!
6 oC -2 oC -4 oC 3 oC 5 oC -10 oC 12 oC -7 oC
Kártyákra írjuk a számokat, majd igazzá tesszük a nyitott mondatot.
Tedd igazzá! Két pozitív értéket
hasonlíts össze! 3 °C; < 6°C
Pozitív és negatív értéket hasonlíts össze! -2°C < 5° C
Két negatív értéket hasonlíts össze!
-7°C < -2°C
Most állítsd nagyság szerint sorba! Melyik évszakra jellemzőek az adatok?
Ha földrajzi magasságként gondolkodunk a negatív számokról, azt mondjuk, nagyobb, ami magasabban elhelyezkedő helyet fejez ki. Lássuk az órarészletet!
Földünk legmagasabb hegycsúcsa 8848 m, az óceán legnagyobb mélysége 11034 m.</span>
Olvashatják a gyerekek az írásvetítőről.
Szövegértelmezés:
- Melyik a legmagasabb hegycsúcs? Csomalugma (Himalája)
- Hány méteres? 8848 m
- A legmélyebb a tenger a Marianna-ároknál.
- Hány méter mély? 11034 m
- Hogyan helyezkednek el a valóságban a tenger és a hegy?
Modellezés írásvetítőn és terepasztalon:
1. A terepasztalon próbáljátok elkészíteni!
2. Rakd ki az írásvetítőn!
3. Hol az óceán? Hol a hegy?
4.Mi van a hegy alatt a valóságban?
5.Mi van az ábrán az üres helyen?
A tengerszint legyen a 0 m magasság!</p>
<p class=lista>Hány méter magas a hegycsúcs? 8848 m</p>
<p class=lista>Hogyan tudjuk matematikai jellel kifejezni </p>
<p class=lista>azt, hogy ez kiemelkedik, magas?</p>
<p class=dvv>+8848 m</p>
<p>A Marianna-árok a tengerszint alatt fekszik. Víz borítja. Milyen vastag
a vízréteg felette?
11034 m</p>
<p>11034 m mély.</p>
<p>Hogyan fejezhetjük ki jellel, hogy ez a
magasság a tengerszinthez</p>
<p>képest lefelé terjed?</p>
<p class=dvv>-11034 m</p>
<p>Tankönyv 109/7. feladatát keresd!</p>
<p>A Csendes-óceán közepes mélysége 4028 m.
Írjuk le a tengerszinthez viszonyított magasságként negatív számmal!
4028 m </p>
<p>Töltsük ki a táblázatot!</p>
Közepes magasság Legkisebb magasság Csendes-óceán -4028 m - 11034 m Atlanti-óceán -3743 m - 9219 m Indiai-óceán -3963 m -7450 m A laphoz nem tartoznak aloldalak.