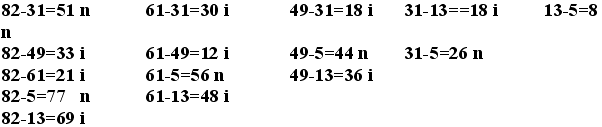Matematika/Tanterv/Valószínűség, statisztika/Valószínűség/Feladatok a valószínüségre
Az Alsós tanítói portálból
Tartalomjegyzék |
Óravázlat a téma tanításának illusztrálására
3. osztály
Téma: Kombinatorika, valószínűség
Tananyag:
Valószínűségi megfigyelések esemény bekövetkezésének valószínűsége. "Biztos", "Lehet, de nem biztos", "Lehetetlen" kifejezések értelmezése, használata.
I. Biztos, Lehet, de nem biztos, Lehetetlen kifejezések értelmezése egyszerű fogadások kapcsán
Szókártyák a táblán
1. 6 kisgyereket kihívunk. Kik használják ezt a szekrényt? Nyitva maradt az ajtaja. Ne nyomozzunk, hogy ki hagyta nyitva! Húzzunk gyufát! Az fogja becsukni, aki a rövidebbet húzza!
Húzzunk! Csukd be!
2. 3 személy (a két hetes és a tanító) között zajlik a játék
Valamelyikünknek ki kell mennie a mosdóba, bevizezni a rongyot. Feldobok egy pénzérmét. Ha fej, X megy ki. Ha írás, Y. Ha fent marad, én megyek ki.
Mondj véleményt a táblán lévő kifejezések segítségével a fogadás feltételeiről.
Lesz biztosan bekövetkező esemény? A pénz leesik. X vagy Y kimegy ,mert vagy fejet vagy írást dobunk.
Lesz olyan esemény, amely lehet, hogy bekövetkezik, de nem biztos? X kimegy, mert fejet dobunk. Y kimegy, mert írást dobunk.
Lesz olyan esemény, amely lehetetlen, hogy bekövetkezzék? A pénz fennmarad. Miért?
II. Valószínűségi megfigyelések együtt és önállóan
1. 5 fehér és 5 fekete zokni van a dobozban. 10 kisgyerek öltözhet fel.
Milyen színűt szeretnél? Biztos olyan lesz? Adok egyet.
Véletlenszerűen kiosztom a zoknikat. A fenti kérdéseket mindegyik esetben felteszem. Figyeljék meg, hogyan változnak a válaszok. Eleinte bizonytalanok, reménykednek, hogy pont olyan lesz. Később megpróbálja megjegyezni, hogy melyikből fogyott több. Amikorra az egyik szín elfogy biztossá válik abban, hogy csak a másikat kaphatja. Abból kér, és diadalmaskodik.
Honnan tudta a társad, hogy . színű zoknit fog kapni? (A megbeszélésen élvezettel avatnak be bennünket a gyerekek saját gondolatmenetükbe.)
2. Édesapa sötétben öltözködik. Benyúl a szekrénybe. Csak 5 pár kék és 4 pár piros zoknija van. Hányat vegyen ki, ha ma kék zokniban akar dolgozni menni?
Mit gondolsz? Össze-vissza elhelyezett kártyák közül kell választania minden eljátszás előtt. Az előbbi tapasztalatok már segítik az előzetes okoskodásban.
Válassz a kártyák közül! Lehet, de nem biztos. Lehetetlen. Biztos.
Minden kártyaválasztás után, többszöri eljátszás következik . Tornazsákból fagolyókat húzunk. Egyszerre emelünk ki egyet, kettőt, hármat, stb. Majd eldöntjük, hogy jól okoskodtunk-e? Úgy alakult-e az esemény, ahogy vártuk?
Az okoskodás-eljátszás-döntés az óra legélvezetesebb része. A második, harmadik eset után már félénk sejtések, bátor intuiciók, magabiztos gondolatok, brilliáns érvelések hangzanak el. A gyerekek élvezettel játszanak és beszélgetnek matematikai megfigyeléseikről.
Íme a megoldás:
1. Lehet, de nem biztos.
2. Lehet, de nem biztos.
3. Lehet, de nem biztos.
4. Lehet, de nem biztos
5. Biztos.
6. Biztos.
7. Biztos.
8. Biztos.
9. Biztos.
3. Végül önálló feladatmegoldás következik. A gyerekek feladatlapon dolgoz-nak. Dőlt betűkkel a megoldást is megadjuk. A gyerekek feladatlapján ez természetesen nem szerepel.
Ellenőrzés felolvasással. Egy-egy döntés indoklása.
Ha óra végén jut idő, álljon itt egy kis töprengenivaló.
Ha csokoládéban játszanánk Zsófi szabálya szerint, és egy állítást választhatnál ezek közül, melyikkel nyerhetnél ezek közül? Mit gondolsz? Miért.
Melyik a biztos vesztes állítás?
Szerinted melyikkel érdemes játszani ezek közül?
Lesz közöttük piros.
Mind piros lesz.
Mind különböző színű lesz.
A megoldáshoz érdemes összegyűjteni az összes lehetséges húzás rajzát.
4. osztály
Melyikből van több?
Számkártyákkal játszunk. A gyerekek két számkártyát húznak ezek közül:
Mielőtt megnéznék, tippeljenek, hogy páros vagy páratlan lesz-e a számok összege.
Melyik lesz gyakoribb? Az összeg párosvagy Az összeg páratlan állítás teljesülése?
Ezután próbálgatnak, és lejegyzik tapasztalatukat. Régebben folytatott megfigyeléseik hamar ráirányítják a figyelmüket arra, hogy bármelyik két számot adják össze, az eredmény páros lesz, mert a résztvevő számok mind páratlanok.
Változtatunk a játékon: betesszük ötödiknek a 36-ot. Hogyan alakul most a játék? Melyik fordul elő gyakrabban: a páros vagy a páratlan összeg?
Most a következő két állítás egyike mellett kell tippelnie:
Összegyűjtik a lehetséges összes páros, illetve páratlan összeget.(Kombinatorikai feladat)
A 13 összeadható a 21-gyel, 29-cel, 45-tel és36-tal
A 21-hez a 29-et, a 45-öt és a 36-ot adhatjuk hozzá.
A 29-hez a 45 és 36 adható.
A 45-höz már csak a 36 adható.
Az összegalakok megfordításainak semmi értelme, mert nem jutunk újabb összeghez. Tehát a kéttagú összegek száma ennek az öt számnak a felhasználásával: 10 Közülük 6 páros és 4 páratlan összeg van.
Tehát az összeg páros állítással van nagyobb esélyünk a nyerésre.
Növeljük nyerési esélyeinket!
Érdekes probléma lehet az esélyek növelése. Szeretnénk úgy változtatni a játékon, hogy egyenlő esélye legyen mindkét játékosnak. Annak is, aki arra fogad, hogy az összeg páros, és annak is, aki arra, hogy az összeg páratlan.
Mit gondoltok, hogyan változtassak a játékban résztvevő számokon?
Gondolkodjanak a gyerekek. Alakítsák át a háromféle állításnak megfelelően a feladatot. Vezessünk be új kártyákat (Például: 44 és 88) Vegyék számba a lehetőségeket, s a szerint válasszanak.
A) A 13, 21, 36 és 50 számkártyákkal számolunk.
Két páros, két páratlan esetében 2:4 -hez a páros-páratlan aránya. (pl. 13+21=pá 13+36=ptlan 13+50=ptlan 21+36=ptlan 21+50=ptlan 36+50=pá)
B) A 13-mal, a 44-gyel és a 88-cal játsszunk.
13+44=ptlan 13+88=ptlan 44+88=ptlan 1:2-höz a páros aránya a páratlanhoz.
C) A 13, az 50, a 44 és 88 vesz részt.
13+50=ptlan, 13+44=ptlan, 13+88=ptlan 50+44=pá, 50+88=pá, 44+88=pá ugyanannyiszor teljesül a páros, mint a páratlan összeg. Tehát a játékban résztvevő számok negyedének páratlannak, a 3 negyedének pedig páros számnak kell lennie, ha igazságos feltételekkel akarunk játszani.
Ezt a játékot is párokban játszhatják a gyerekek: 31, 49 61 5 82 13a játékban szereplő számok. Összekeverés után kettőt kell húzni. A húzott két szám különbségét kell kiszámolni, majd eldönteni, hogy a különbség osztható-e 3-mal. 10 húzásról feljegyzést kell készíteni, majd 10-es sorozatokra előre tippelni kell, hányszor lesz 3-mal osztható a különbség. Az nyer, akinek a tippje a legjobban megközelítette a bekövetkezést. Több sorozat játék után a magyarázatot is kereshetik.
Alkossuk meg az összes felírható kivonást! A nagyobb számból veszünk el! (A gyerekek például a 31-82 kivonással nem tudnak mit kezdeni.)
Kilenc esetben teljesül, hogy a különbség osztható 3-mal és hat esetben nem. Ez 9:6-hoz arány. Az tippel jól, aki az igenre nagyobb esélyt jósol. Ennél finomabb megközelítésre nincs szüksége a kisgyereknek.
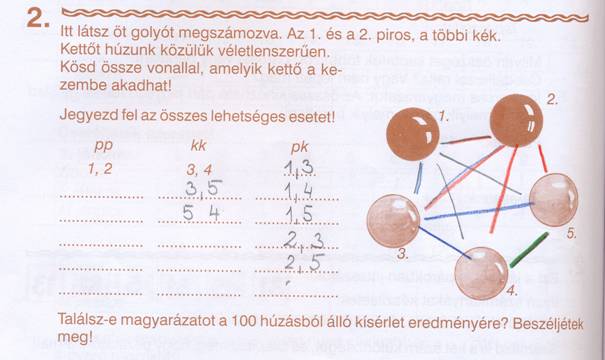
Sok más golyókkal játszható játékot is kínál a munkafüzet. Két piros és 3 kék golyó közül kettőt húzunk. (Munkafüzet 112/1.)
Grafikonon ábrázoljuk, hogy 100 húzás közül hány p-p, k-k és p-k húzás lesz.(Lásd Statisztika téma!) Általános megfigyelési feladat, inkább csak az újszerű ábrázolásmód, a regisztrálási módszer kedvéért oldjuk meg.
(Munkafüzet 112/1)
A következő feladat már megkülönbözteti azt az öt golyót számozással, amelyek közül kettő piros, és 3 pedig kék. Megfigyeljük azt, hogy összesen hányféle lehetőség van az 5-ből a kettő egyszerre való kiválasztásának. A lehetőségek számbavétele után tud dönteni a kisgyerek arról, Melyik a gyakoribb esemény: pp, kk, vagy pk húzása?
párból 1 pp, 3 kk és 6 pk lesz. (Munkafüzet 112/2.)
Ezután elgondolkodunk azon, hogy legalább hányat kell kivennünk, hogy legyen köztük piros, legyen kék, legyen két azonos színű… stb. (Munkafüzet 112/3)
Sokféle játék áll még rendelkezésünkre. Csak akkor fogjunk hozzá, ha elegendő időt tudunk adni arra a gyerekeknek, hogy kedvükre végezzék a megfigyeléseket. Tanítsuk meg őket arra, hogy a környezet legegyszerűbb tárgyaival is lehet ilyen játékokat játszani. Lehet a rózsaszín rúd leesését figyelni. Vajon a négyzet vagy a hosszúkás téglalapján áll-e meg. 500 ejtés után már alakulhat elképzelése. Lehet piros-kék korongokkal, vagy pénzérmék feldobásával játszani. Játsszunk sokat, mert „a játék az gömbölyű” !
A feladatok egy része C. Neményi-Káldi 4. osztályos tankönyvéből és munkafüzetéből valók.
C. Neményi-Káldi Matematika munkafüzet 4. osztály
A laphoz nem tartoznak aloldalak.