Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Számfogalom - a számfogalom tapasztalati alapjai/A számkör, a számkörbővítés/Számfogalom a 3. osztályban
Az Alsós tanítói portálból
Tartalomjegyzék |
Ismerkedés az 1000-es számkörrel
Október közepén kerítünk sort a számkörbővítésre. A számkörbővítés a 3. osztályban is szemléleti alapon történik. A számfogalmat eddig is kétféle típusú tapasztalatra építettük. Az egyik a darabszám, a másik a mérésből adódó mérőszám. Ennek megfelelően meg- és leszámlálásokkal kezdünk. Tapasztalatokat szerzünk az 1000-es számkör számairól, akár darabszámról, akár hosszúságról, időről, tömegről, területről van szó. A számkörbővítéshez tartoznak a konkrét mérések és átváltások is. Célunk, hogy a számok a gyerekek gondolataiban valóságtartalommal teljenek meg.
Számlálások egyesével, kettesével, ötösével, tízesével, húszasával, ötvenesével,...pontosan és közelítéssel
A megszámlálásokhoz, leszámlálásokhoz mindent fölhasználunk, amit csak a környezet nyújt: terméseket, a mesekönyv betűit, pénzérméket, stb. Bár tudjuk, hogy a 45 perces tanóra alatt még háromezerig sem jutnánk az egyesével való számlálásban, mégis kezdjünk bele az egyesével való számlálásba.
Házi feladatként gyűjtőmunkákat adhatunk. Hány lépésre laksz az iskolától? (egyesével kell számlálnia) Hány autó megy el az ablak előtt 3 perc alatt? Megtanítjuk a strigulázás módszerét, amely szerint négy álló egyenest áthúzunk egy fekvővel, két csoportot átfogva tízesével számlálhatunk. Ez már csoportosítva számláláshoz vezet, de a gyerek még látja a valódi mennyiséget is.
A csoportosítások, csoportosítva számlálások vezetnek a számrendszeres gondolkodás felé. Kisebb csomagokat képeznek, ezeket a csomagokat újra továbbcsomagolják nagyobb kupacokba. Így gyorsítva meg a darabszám megállapítását. (Munkafüzet 35/2.)
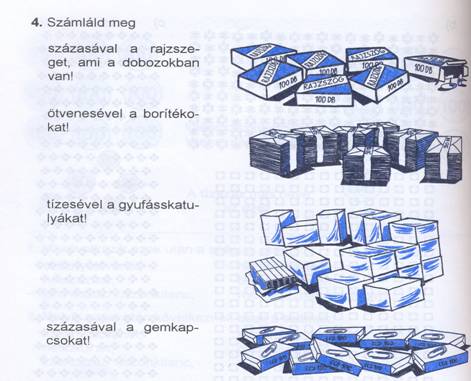
Csomagokat számláltatunk: a postai levélborítékot ötvenesével, a gyufaskatulyákat tízesével csomagolják. A papírzsebkendőt százas és tízes csomagokban is árulják. Jó még a gemkapocs, tűzőgép kapcsa, Milton-kapocs, sokféle Ápisz-áru. (Tankönyv 64. oldal)
Közelítés, közelítő érték, közelítő pontosságú mérés
Kupacok alkotásával számlálhatják meg a rizsszemeket (2-4 dkg rizs körülbelül 1000 szem). Sürgessük a gyerekeket, hogy keressenek olyan módszert, amivel minél hamarabb megmondhatnák, hány szem van előttük. (Ezzel előkészítjük a közelítő számlálást is.)
A közelítés gondolata újdonság a harmadik osztályban. A fárasztóan egyhangú leszámlálások közben rájön a kisgyerek, hogy nem minden esetben kell tudnunk pontosan, hogy valamiből mennyi van. Elég lehet, csak éppen megközelítően, körülbelül megadnunk. Jó módszereket kell adnunk a közelítő számlálásra.
Nemcsak a leszámlálási módszerek miatt érdemes jól kidolgoznunk a közelítő számlálást, hanem mert majd később a műveletek eredményének előrevetítéséhez, a becsléshez alapfeltétel lesz, annak a szemléletnek a megléte, hogy elfogadható a közelítő pontosság. A számfogalom tartalmának új eleme ebben az évben a közelítő szám. Ezt a tartalmat a számlálások mellett leglátványosabban az adott pontosságú mérésekkel alapozhatjuk meg. Annak a tapasztalatnak a megszerzése igen fontos, hogy gyakran elegendő közelítő pontossággal megadni egy tárgy méreteit. A tanterem körülbelül 7 m széles, a ceruza körülbelül 10 cm hosszú stb. (Lásd: Mérések!)
A meg- és leszámlálások, a gyakori meg- és kimérések következtében eljutunk az elvont számokig. Természetesen nem mindegyik gyerek számára ugyanabban a pillanatban, de egy-egy szám tüzetesebb megvizsgálásakor egyre gyorsabban épül ki a kapcsolat a konkrét tartalom és az elvont szám között. Fontos feladatunk most a számok nevének és leírt alakjaik épülési rendszerével megismerkedni. Sokszori különféle kirakás után érdemes eljutnunk oda, hogy csak százas, tízes, egyes pénzérmékkel is kirakjuk a számokat. Azért éppen ezeket használjuk alapérmékül, mert ezek reprezentálják legjobban a tízes számrendszer épülését. Az egyes érmékből csak 9 darab áll a rendelkezésünkre, mert amint 10 összegyűlik valamiből, azonnal váltanunk kell a legközelebbi nagyobb egységre.
Tevékenységek
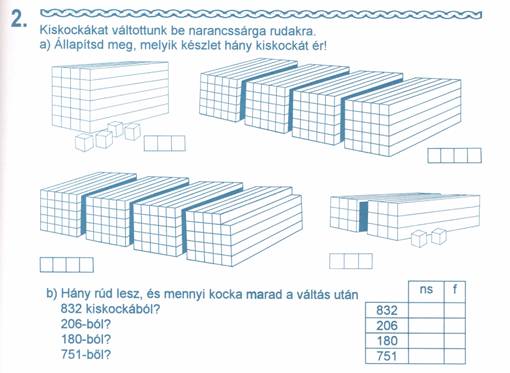
Számfelismerés kirakásokról ( Például a 460 kirakható négy narancssárga és egy lila rúd segítségével, ha a fehér rúdnak 10-es értéket tulajdonítunk. Használhatunk játékpénzeket, papírzsebkendőket, bármit, ami valahányasával csomagolt áru.
Ezek leolvasása, majd lejegyzése
Számjegyírás, diktálás után
Különböző számok megjelenítése kirakással vagy más módon. A gyerekek ötletesek ebben a tevékenységben. A 510 például megjeleníthető mérőszalagon 510 mm kijelölésével, a könyv 510 oldalának fellapozásával, kirakható színes rúddal, játékpénzzel Milliméterpapíron is jól megjeleníthető a szám a maga valóságos alakjában. Tízes csíkokból, százas négyzetek, azokból ezres nagyobb csíkok épülnek.
Videó: Az 510 megjelenítése sokféleképpen
Gyűjtések: Mit lehet kapni 510 Ft-ért? Stb.
Az abakusz is hasznos eszközünk lehet. Ez már kissé elvontabb helyiértékes alakját mutatja számnak
(Munkafüzet 43. o.)
Bontások: Bontsunk fel számokat helyiérték szerint (234=2 sz+3t+4e vagy 2 sz+2 t+14e vagy 1sz+13t+4e vagy 1sz 1t 24e, stb. Ismerjen rá, hogy ez ugyanaz a szám sokféle bontásban!)
Ismerje fel a sokféleképpen bontott számokat, s írja le egy számalakban.
Ne csak helyi- hanem valódi értéke szerint is bontsa a számokat. 234=200+30+4 Ez a fajta írásmód sokat fog majd segíteni a szó-és írásbeli műveletek előkészítésénél is. Most a szám valódi értékének megítélésében van nagy szerepe.
A számtáblázatok is hasznosak a számfogalom építésében, mert a rendszerszemléletet erősítik. (Munkafüzet 46. o.)
A számsorozatok alkalmasak arra, hogy a kisgyerek lépésenként tágítgassa látókörét a számok között. Az egyenletes növekedés, csökkenés közben felfigyel a számok változásainak ritmusára, s fontos megfigyeléseket tehet a szabály követése közben. Ha ez számegyenesen való lépegetéssel is kiegészül, a gyerek valóságos tapasztalathoz jut a számok nagysága, egymástól való távolságuk, viszonyuk terén.
A számrendszeres gondolkodás alapozása
Nagy hasznát vesszük az első-második osztályban elkezdett kisebb számrendszerekkel való ismerkedésnek, a csoportosításoknak és beváltásoknak. A kisebb számrendszereken megértett csoportosítási elvre épülhet a tízes számrendszer tízesével való csoportosításának elve. A számrendszer és helyiérték-rendszer jó megértéséhez hozzátartozik annak tudatosítása, hogy egy tetszőleges szám 1, 2, 3, hellyel való balra tolása a helyiérték-rendszerben azt jelzi, hogy nagyobb értékű csoportokból van az adott szám. Fontos tudatosítanunk a nulla helypótló, helyfenntartó szerepét is.
Számok helye a számegyenesen
Kezdetben készíthetünk érdekes számegyeneseket is. A papírzsebkendő számegyenes előnye, hogy még kézzelfogható, valóságos mennyiség van mögötte. Ezt követhetik a számvonalakon, számegyeneseken való lépkedések. Ötösével, tízesével, húszasával, ötvenesével, százasával beosztott számegyeneseken tájékozódunk. Megjelölünk rajta számokat, illetve az ott lévő jelölésről megállapítjuk, melyik számot takarhatja.
Fokozatosan alakítjuk a számegyenes beosztásait. Egyre ritkítjuk. Egy-egy számra lassan közelítünk rá. Legjobban a nagyító példájával tudjuk a gyerekekkel megértetni, hogy szabad szemmel nagyon jól látjuk a százast jelző beosztásokat, a tízesek kis nagyítással láthatóvá lesznek, erős nagyítással még az egyesek is jól kivehetők. Megfigyeltetjük, hogy a szám első számjegye azt mutatja meg, hogy melyik százas szakaszon, a középső számjegy a tízes részletet és az utolsó számjegy a pontos helyet jelöli meg. Sokat segít az egyes, tízes, százas számszomszédok megkerestetése is. Ezzel már a kerekítést is előkészítjük.
A kerekítés
Könnyen belátja a kisgyerek a kerekítés szükségességét, hiszen ha megkérdezzük tőle, hogy mennyibe kerül egy kakaós sütemény vagy egy dobozos üdítőital, máris százas számkörben megjelöl egy kerek számot. Azt mondja ösztönösen, hogy körülbelül 170 Ft vagy 200 Ft körül. Azért tesz így, mert nem emlékszik pontosan. Gyakran ha tudják is a pontos árat, hamar meg kell állapodnunk egy körülbelüli közeli számban, mert nem ugyanazon a helyen vásárolnak, és akár 20-30 forintos eltérések is lehetnek a különböző árak között. Könnyen rávezethetők a kerekítés szabályaira a számegyenes használatával és a számszomszédok kijelölésével. Hamar észreveszik, hogy ahhoz a százashoz, tízeshez érdemes kerekíteni, amelyhez a szám láthatóan közelebb áll. Problémát csak az jelenthet, hogy mi legyen a pontosan középen, azaz a mindkét számtól egyenlő távolságban elhelyezkedő számokkal, az 50-nel és az 5-tel. Igyekezzünk úgy alakítani a beszélgetést, hogy a gyerekek maguk ajánljanak valamiféle megállapodást: kerekítsük őket felfelé! Ne kerekítsük! Kerekítsük a kisebb százashoz! stb. Akadálya lehet ennek az, ha van nagyobb testvér, akitől elleshette a szabályt, esetleg a szülő megmondta neki, mert már előbb ráérzett a gyerek erre a problémára. Nem szabályt akarunk velük bemagoltatni, hanem olyan kerek százast vagy tízest keresünk, amely a lehető legjobban reprezentálja számot.
Izgalmas feladatok sokaságát kínálja a téma:
Legyen a fehér kocka értéke 100! Színes rudakkal rakd ki közelítőleg ezeket a számokat: 301, 788, 291, 600, 226, 150, 947, 817! Legyen most a fehér értéke 10! Most ezeknek megfelelő közelítő hosszúságot rakj ki: 120, 176, 69, 217, 134, 381, 222, 105!
Engedjük a gyerekeket vitatkozni azon, hogy a 105-öt mi reprezentálja inkább a 100-nak megfelelő narancssárga rúd vagy a 110-nek megfelelő narancssárga és fehér. Vegyék észre azt is, hogy a kerek számok közelítő értéke egyben önmaguk.
Keress olyan számokat a számegyenesen, amelyeknek tízesekre kerekített értéke 150!
Vegyék észre, hogy a kijelölt szakaszon a 150 is rajta van!
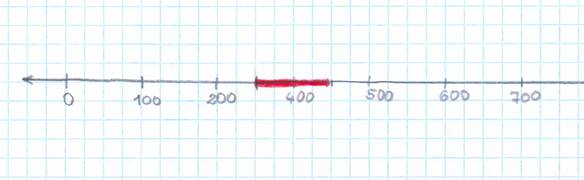
Színezd pirosra a számegyenesnek azt a szakaszát, ahol azok a számok találhatók, amelyeknek százasokra kerekített értéke 400! Olvass le ilyen számokat!
Itt a színezett szakaszon a 400 is rajta lesz. Beszéljünk erről is, mert hasznos tapasztalat!
Szöveges feladatok segítik a probléma mélyebb megértését, és ezek a matematikai szóhasználat értésének és használatának begyakorlására is alkalmasak.
5. Levágtam egy körülbelül 400 mm-es papírcsíkot. Tudom, hogyha leírom számjegyekkel a pontos értékét, a tízesek helyén a 7-es számjegy áll. Mekkora lehet a papírcsík hossza?
A szövegértelmezésnek az alábbiakra kell kiterjednie. Egy vagy több megoldása lesz a feladatnak? Hány jegyű számokról van szó? Honnan tudja? (Négyszáz körüli szám, tehát legkevesebb 350 és legfeljebb 449 lehet) Melyik szám kerülhet a százasok helyére, ha a tízesek helyén a 7 áll? (csak a 3 jöhet szóba, mert a négyszázhetvenvalamennyiről nem mondaható el, hogy négyszáz körüli)
A szóba jöhető számok:370, 371 .... 379,
6. Egy számra gondoltam. Nincs messzebb a 380-tól, mint 25 egység. Mennyi lehet a százasokra kerekített értéke?
Számegyenes segítségével oldhatja meg a feladatot, s rájön, akár jobbra, akár balra lép a számegyenesen 25-öt a 380-tól nem lép ki a 400 körüli számok köréből. A gondolt szám pedig sokféle lehet. Nem baj, ha nem soroljuk fel mindet, de jelöljük ki a szóba jöhető legkisebb és legnagyobb számot, s állapítsuk meg, hogy ezek közt van a gondolt szám.
Egy 3-ra végződő számot százasokra kerekítek. A százasokra kerekített értéke 600. Mi lehet a szám?
Szövegértelmezés: Hány jegyű számról van szó? Ismerjük-e valamelyik számjegyét? - - 3
Mit tudunk még róla? 600
Mutassa meg a számegyenesen, melyek azok a számok, amelyeket 600-ra kerekítünk! 550 -től 649-ig
Melyeket kerekítjük lefelé?
Mely számok kerülhetnek a tízesek helyére? 0, 1, 2, 3, 4. Az 5 már nem.
603 613 623 633 643
Mutassa meg a számegyenesen, melyek azok a számok, amelyeket felfelé 600-ra kerekítünk!
Mely számjegy állhat még a százasok helyén? 5
Mely szám kerülhet a tízesek helyére? 5, 6, 7, 8, 9
553 563 573 583 593
Ellenőrzésképpen egy-egy kiválasztott szám kerekítését elvégezzük és leírjuk.
Gondoltam egy számot. A százasokra kerekített értéke 10-zel kisebb, mint a tízesekre kerekített értéke. A százasok helyén 3 áll. Mi lehet a gondolt szám?
305, 306, 307, 308, 309, mert százasokra kerekített értékük 300, de a tízesekre kerekített értékük 310 és a kerekített értékek között pontosan 10 a különbség.
A gondoltam egy számot típusú feladatok nehezek, mert egyszerre többféle szempontot kell a gyermeknek észben tartania, s a kerekítéssel kapcsolatos ismereteit alkalmaznia kell tudni, de ha lépésenként adjuk a feladatot, közösen meg tudjuk oldani. Haszna, hogy mintát adunk az analizáló-szintetizáló feladatértelmezésre. Kellő gyakorlat után maga is meg fog tudni oldani hasonló feladatokat.
A számképzés
Az ezres számkör kidolgozása idején a gyerekeknek igen kedves kombinatorikai feladatokat is a témához rendeljük. Igaz, hogy ezekkel elsősorban a kombinatorikus gondolkodásmód kialakítása a célunk, de ehhez jól illeszthető a számokról tanultak folyamatos gyakorlása, ismétlése.
Feladatok:
Letakartam egy háromjegyű szám első jegyét.
Melyik szám lehet ez? Élje át a csereberélés élményét. Háromszögletű lapokra írjuk a számjegyeket, s rakosgassa a kisgyerek. Gyűjtsük össze az össze lehetséges számot! Hányféle megoldás van?
2. Ez melyik szám lehet:5∆2 ? Hányféle megoldás van? Miért van eggyel több, mint az előző feladatnál? A 0 szerepelhet a tízes helyen, de a százas helyen az előzőnél nem kaptunk volna háromjegyű számot.)
3. Két háromjegyű számot takartam le. Az azonos alakú lapok azonos számjegyeket jelentenek.
∆3◄∆4◄ Mely számok lehetnek ezek? Melyik nagyobb? Mennyivel?
Hasznos tapasztalat lehat, ha nagyon sok számpár összegyűjtésével önállóan jutnak el a gyerekek a felismeréshez: a második szám mindig tízzel nagyobb. Probléma lehet, hogy gépiessé válik a számképzés és a 838 is megjelenik. Fel kell hívni a figyelmet, hogy nem állhat egyforma szám a százas és egyes helyen, mert nem egyformák a takarólapok.
Nagyon fontos a mobil számkártyák használata a számképzéseknél Számjegyek állnak a kártyákon. Egy kártyán egy számjegy. Lehet ez alkalmi készlet is, amit a gyerek írólapból ott és akkor készít el. Így jobban megérti a felhasználható alaphalmaz lényegét. Azok a kérdések, hogy hányszor használható fel egy kártya, önmaguktól megoldódnak. Négy darab számkártyából: 2, 3, 4, és 5-ösből kell kétjegyű, háromjegyű és négyjegyű számokat alakítani. Nyilvánvaló, ha igazi kártyával dolgozik a kisgyerek, nem tudja kirakni a 227-t. Ha sok 2-es és 7-es számkártyával dolgozik, akkor igen. Hasznos, ha a születő számokat kis cédulákra írja, mert akkor ezek elrendezhetőek. Nem várható el a korosztálytól, hogy azonnal rendszeres, tervszerű gyűjtésbe fogjon, de a mozgatható kártyákkal utólag kialakítható a rendszer. Értékelni kell a rendszerre törekvést a gondolkodásban, mert ezt akarjuk kialakítani, de ügyeljünk, hogy ne siettessük a lassabban haladókat.
1.: A 0, 1, 2, 3, 4, 5 számjegyek felhasználásával képezz háromjegyű számokat! Ha kártyával dolgozik, természetes, hogy csak egyszer használhat felé egy kártyát, ha papíron írja a számokat, akkor külön feltételként kell ezt megszabni. Így nagyon sok számot tud felírni. Nem kell valamennyit megtalálnia. Arra azonban jó a feladat, hogy felébressze a rendszerképzés igényét.
2.: Ha ugyanezekből a számjegyekből kell olyan háromjegyűeket előállítani, amelyben a számjegyek alaki értékeinek összege 5, akkor jelentősen szűkül a lehetőségek száma. Azt kell észrevenni, hogy az 5 háromtagú bontásaiból kell kiindulnia: 1+4+0, 2+3+0 illetve 5+0+0, s ezek sorrendjét cserélgetni. Tehát:
401, 410, 104, 140,
302, 320, 230, 203 és 500 a keresett számok.
Kisebb alaphalmaz esetén már a rendszerképzésre is van lehetőség, mert keveset könnyebben áttekint a kisgyerek.
A 2, 3, 4-es számjegyekből az összes lehetséges háromjegyű kirakásához használhat fadiagramot. (Ha kártyákkal rakosgat, egyértelmű, hogy egy kártya egy számban egyszer szerepelhet, ha ír, akkor a feltételt külön közölni kell. Ha nincs benne a feladatutasításban ez a feltétel, egyértelmű, hogy az ismétléses eseteket is le kell írnia. A pedagógus felelőssége a pontos utasítás megfogalmazása!)
Az ismétlés nélküli esetekhez belehelyezkedhetünk a helyiérték-táblázatba. 6 ilyen szám lesz.
Ismétléssel megsokszorozódik a lehetőségek száma. Ehhez már valóban elengedhetetlen a fadiagramos ábrázolás.
Ügyes eszközünk lehet az írásvetítőre tehető mozgatható számjegyű számváltoztatós, mert alkalmas minden szám rendszerszerű előállítására. Használjuk, de a lejegyzéshez fadiagramot vagy táblázatot alkalmazzunk. A számleolvasást külön gyakoroltassuk!
C.Neményi- Wéber: Matematika tankönyv és Munkafüzet 3. osztályosok számára
A laphoz nem tartoznak aloldalak.