Matematika/Tanterv/Gondolkodási műveletek/Halmazok, logika
Az Alsós tanítói portálból
Tartalomjegyzék |
Válogatások
Már első osztályban az előkészítő időszaknak a legfontosabb tevékenységi formája a még később is jelentőséggel bíró válogatások. A tárgyak, személyek, halmazok sokféle összehasonlításával, osztályozásával, sorba rendezésével elindíthatjuk a gyerekeket a tudatos tapasztalatszerzésben, tudatos megfigyelésben és a megfigyeltek kifejezésében, rögzítésében. Általában könnyebb a gyerekek számára a saját maguk által kitalált szempont szerinti válogatás, kissé nehezebb a tanító által megadott válogatási szempont átvétele. Még nehezebb feladat a megkezdett válogatás folytatása, mert ott a válogatás szempontjául választott tulajdonságot kell felfedezni először, majd a tulajdonság szerint új elemeket keresve folytatni a válogatást. Kétfelé válogatás
A harmadik osztályban tudatossá tesszük, hogy egy tárgynak, személynek válogatáskor csak egy helye lehetséges. Vagy beletartozik a részhalmazba vagy ezen kívül való. A címke feliratozása szigorú szabály szerint történik, kifejezi, hogy a részhalmazba tartozók mind ilyenek, a kívül maradók pedig nem rendelkeznek a tulajdonsággal, azaz nem ilyenek. A címkén lévő tulajdonság vagy fogalom
- a rész minden elemére igaz
- minden kint lévőre pedig téves.
A válogatás során mondhatjuk úgy is,
- a részbe csak ilyen tulajdonságú elemeket lehet tenni
- de az összes ilyen tulajdonságút ide kell tenni.
Példa: válogatáskor a tejtermékek közé az összes tej alapanyagú készítmény bekerül (tej, sajt, vaj, …), de egyetlen kint maradó termék (szalámi, kenyér, alma) sem lehet tej alapanyagú.
Kétszer kétfelé válogatás
1. Kétféle szalagkarika kerül a földre. A piros karikán ez a címke van: lány, a kéken: fiú. A gyerekek beleállnak a megfelelő körbe. Ellenőrzésképpen megbeszéljük:
-Csak lány áll a piros karikában? Minden lány ott van? -Csak fiú van a kékben, az összes fiú ott van?
A gyerekek vagy lányok vagy fiúk. Egyetlen olyan gyerek sem lesz, aki egyszerre két helyen állna.
2.A piros karikára most a lány, a kékre a szemüveges felirat kerül. Így nem lesz helye annak a kislánynak, aki szemüveges. Az ellenőrzésnél fel is erősítjük a problémát: -Minden lány a piros karikában áll?
Ez csak úgy teljesül, ha minden lány a másik karikán kívül, a nem szemüvegesek között áll. Lesz, aki ijedten átszalad majd a pirosba, mert ő lány is és szemüveges is. De így sem áll jó helyen, mert így a szemüveges tulajdonság vész el. A probléma megoldását hagyjuk a gyerekekre. Közelíteni fogják a karikákat. Megpróbálnak a lányok egyik lábukkal a pirosban, másikkal a kékben állni. Ha rászólunk, hogy döntse el végre, melyiket választja, rákényszerül arra, hogy behúzza egyik karikát a másikba, mondván: a pirosban és a kékben egyszerre áll benne.
Az „és” két állítást kapcsol össze, azaz két tulajdonságot kell egyszerre figyelembe venni a válogatásnál. Nagyon fontosnak tartjuk, hogy ebben a korai szakaszban ne emlegessünk a gyerekeknek halmazelméleti szakszavakat (alaphalmaz, részhalmaz, kiegészítő-halmaz) mert ez még túl korai absztrakció lenne. Válogassunk kosárba, dobozba, karikába. Állításokat is ezekről, s a válogatásban szereplő konkrét dolgokról fogalmazzunk csak.
Az eljátszásokat követően tárgyak válogatásával folytatjuk a munkát. A válogatásokhoz készletekre van szükségünk. A készletek lehetnek alkalmi és véletlenszerűek vagy tudatosan megtervezettek, adott szempontokból összeválogatottak.
Készletek
Kincses doboz
Néhány tárgy a Kincses dobozból
Ebbe a dobozba mindenféle tárgyat összegyűjtünk a gyerekekkel. Különféle játékokat, üres dobozokat, terméseket, szívószálakat, fonalakat, zsinegeket, használati tárgyakat teszünk bele. Készletet rögtönzünk a rendelkezésre álló tárgyakból, s máris kezdődhet a válogatás.
Válogatási szempont lehet bármely tulajdonság
- a tárgyak színe,
- anyaga,
- eredete,
- alakja,
- nagysága,
- felhasználása, s folytathatnánk a sort.
Ügyeljünk arra, hogy mindig kis elemszámú készleten válogassunk a gyerekekkel. Csak jól áttekinthető mennyiségű tárgyon lehet eredményes a válogatás. Tartsuk szem előtt, hogy a válogatás szempontját nem tudják a gyerekek túl sokáig megjegyezni, ezért válogatás közben többször hangozzék el, hogy egy-egy tárgyat mely szempont szerint helyezett a gyerek ide vagy oda.
Logikai készlet
2x3x4x2=48 darabos készlet
Felhasználási lehetőségek:
- Színek, alak, nagyság és felület felismerése
- Utánzó kirakások – házat, kutat, fát, vonatot, emberkét, stb. rakunk ki a táblára, eleinte egyszerre csak egyet, s megkérjük a gyerekeket, hogy rakják ki ugyanezt. Kapnak olyan rajzokat is később, amelyeken a formák méretarányos rajza van. Ezekre, a megfelelő logikai lapokat kiválasztva, rá kell fektetni, lefedni, míg ugyanazt a képet nem látja maga előtt.
- Egyszerű transzformációk – amit kiraktunk csupa kis logikai lapokból, rakja ki a kisgyerek nagyokból. Vagy ami a mintán sima, az ő kirakásán legyen lyukas.
- Szabályjátékok – készíthetünk hozzá kartondobozból „gép”-et. Amit a tanító bedob, benne marad a dobozban, s helyette egy másik esik ki a „gép”-ből. A kisgyerek a saját készletével játszik. Amit bedobtunk, a saját táblázatán balra teszi, ami kijött, azt jobbra. Az előre kigondolt szabály szerint folytatjuk a játékot. Hasonlítsa össze, s ismerje fel a változást. Mondja meg ő, hogy mit fog kidobni a gép. Végül megfogalmazhatja a szabályt is.
- Válogatások
- Megkezdett válogatások folytatása
- Rontó játék – valamilyen szempont szerint összeválogatunk lapokat. Ezek együtteséről mondanak a gyerekek igaz állításokat. Majd úgy kell változtatni a kitett lapokon, hogy a mondat tévessé váljék.
- Barkochba játékok – eldugunk egy lapot. A gyerekek kérdeznek. Csak igennel vagy nemmel válaszolunk aszerint, hogy eltalálták-e az eldugott lap tulajdonságait. A játék végére a gyerekek kitalálják az eldugott lap összes tulajdonságát. Ekkor megmutatjuk az eldugott lapot.
- Rakosgatós barkochba – minden gyerek előveszi a logikai lapjai egy részét (pl.. a kis lapokat). Egy-egy kérdés után mindig szétválogatják a lapokat és visszateszik a dobozba azokat, amelyek biztos nem lehetnek a játékvezetőnél eldugva. Addig ismétlik a rakosgatást, míg csak az eldugott lap marad előttük.
- Néma barkochba – felrajzoljuk a kérdéseket és a feleleteket a táblára. A jelek olvasása, értelmezése után a gyerekek kitalálják az eldugott lapot.
A gondolt lap a sárga, kicsi, lyukas, négyzet.
- Fordított barkochba – jelkártyákat dugunk el. A rajta jelzett tulajdonság a készlet némely tagjára igaz, másokra nem. A játékosok a jelkártyákkal felemelésével kérdeznek. Igennel vagy nemmel válaszolunk. A válasznak megfelelően kell különválogatni a a felmutatott lapokat. Így lehet kitalálni, hogy mi van az eldugott jelkártyán.
- Memória játékok
- Sorozatok(periodikus, egy- vagy többkülönbséges)
- Igaz, hamis állítások gyűjtése – a matematikai logika nyelvi alapjainak lerakása
- Nyitott mondatok
- Később bontások kifejezésére
- Törtek – egységtörtek, egységtörtek többszörösei
- Negatív számok – adósság és vagyon cédulák
- Alakzatok kirakása
- Tükrözések
- Testek építése
- Testhálók készítése
- Kerület, terület, felszín vizsgálata
Autós kártya
A 12 darabos (2x3x4) készlet C. Neményi Eszter-Sz.-Oravecz Márta: Matematika munkafüzet általános iskola 1. osztály című könyvének mellékletében található. A használatával kapcsolatos útmutató C. Neményi Eszter-Sz.-Oravecz Márta: Útjelző az 1 osztályos matematika tanításához című kézikönyvében lelhető fel. (Nemzeti Tankönyvkiadó)
Ugyanolyan “szabályos készlet”, mint a logikai játék. Néhány jellemző darabot kiteszünk a gyerekek elé, okoskodják ki, hány darabból áll a készlet. Ezután bemutatjuk az egész készletet. Jelkártyákat készítünk, tagadással is. Játszhatunk Néma Barkochba játékot is. Memória játék játszásánál is felhasználhatjuk. Ilyenkor két készlettel játszanak a gyerekek.
Katicás készlet
3∙2∙2=12 darabos készlet
A készlet háromféle színű, masnis és nem masnis, gombos és nem gombos katicabogarakból áll. Hány elemű lehet a készlet? Játszható vele Ki vagyok én? játék. Fordított Barkochba játék. Lehetséges még az elemeke bővítése is. Például: Legyenek zöld katicák is!
Üveges készlet
3∙2∙2=12 darabos készlet
A teli, félig töltött és üres; címkés és címke nélküli, rongy kupakos és rongy kupak nélküli darabokból álló készlettel bekötött szemmel is játszhatnak a gyerekek, hiszen a tulajdonságok kitapogathatók, hallhatók. Az üveg nehéz vagy könnyű volta, a folyadék kotyogása elárulja, hogy teli, félig van vagy éppen üres az edény. A tetején tapintható a rongy vagy a műanyag felület. Alkalmas a készlet arra, hogy sokféle érzékszervet dolgoztasson meg.
3-4. osztályban használható készletek
A gyerekek szívesen foglalkoznak a különböző logikai készletekkel. Már első és második osztályos korukban is képesek egyszerű készletek alkotására több-kevesebb tanítói segítséggel. Harmadikban és negyedikben fokozottan ösztönözzük a őket, hogy ne csak megfigyelni legyenek képesek az egyes logikai készleteket, ne csak kiszámítani tudják, hogy hány elemből állhatnak, hanem alkossanak is ilyeneket. A gyerekek igen találékonyak, sokféle ötlettel gazdagíthatják eszköztárunkat. Miközben alkotnak, gondolkodásuk összerendezettebb, szempontkövetőbb lesz.Fejlődik kreativitásuk. A tervezéssel tudatosságuk növekszik. A megvalósítás során kitartónak kell lenniük.
Gyerekkártya készlet
16 darabos készlet.
16 darabos készlet.
Vegyük számba a tulajdonságokat!
- Fiú-lány;
- szőke-barna;
- szemüveges-nem szemüveges;
- szomorú-vidám.
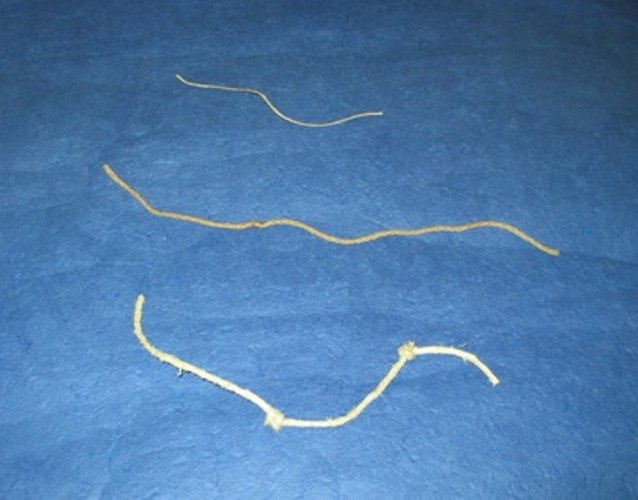
Madzagos készlet
Következtetés néhány elem ismeretében a készlet egészére. 18 darabból álló készlet.
Megmutatom a logikai készletem három darabját. Ki tudjátok találni, hány darabos a készletem? Milyen elemek vannak még benne?
- Csomó nélküli (0 csomós) vékony spárga,
- egycsomós hosszú közepes vastagságú spárga,
- és egy kétcsomós hosszú vastag spárga.
A tulajdonságok a következők:
a spárga vastagsága: vékony, közepes vastagságú, vastag;
a csomók száma: nincs csomó (0), 1 csomós, 2 csomós;
hosszúság: hosszú, rövid;
a készlet 3∙3∙2-es, azaz 18 darabból áll. Készítsük el! Háromféle vastagságú spárgára és ollóra van szükségünk hozzá.
Ha zacskóba tesszük a készletet, s onnan húzunk, kitapogatható logikai készletet alkottunk.
Házikós logikai készlet
16 darabos készlet
Megfigyeltetjük a megkezdett kétszer kétfelé válogatást Mely tulajdonságok fedezhetők fel? Hány elemből áll a készlet?
Tulajdonságok:
- A ház földszintes vagy emeletes (2);
- a ház piros tetejű vagy barna tetejű (2);
- kertes vagy nem kertes (2);
- a háznak egy vagy két ablaka van (2).
A készlet 2∙2∙2∙2=16 darabból áll.
Könnyen elkészíthetik a gyerekek is akár önálló rajzolással, akár előre megrajzolt ábrák színezésével.
Használható kétfelé és kétszer kétfelé válogatáshoz.
Learning by logic
60 darabból álló készlet (Angol logikai készlet a hazai megszokott tanszergyártók és terjesztők kínálatából, barátságos áron megvásárolható.)
Ismerkedjünk meg a készlettel!
Tulajdonságok: nagyság, vastagság, szín, alak
- Nagyság: kicsi, nagy (2)
- Vastagság: vastag, vékony (2)
- Szín: piros, kék, sárga (3)
- Alak: háromszög, négyzet, téglalap, hatszög, kör (5)
A készlet 2∙2∙3∙5=60 darabból áll. Sokféle játék játszható vele.
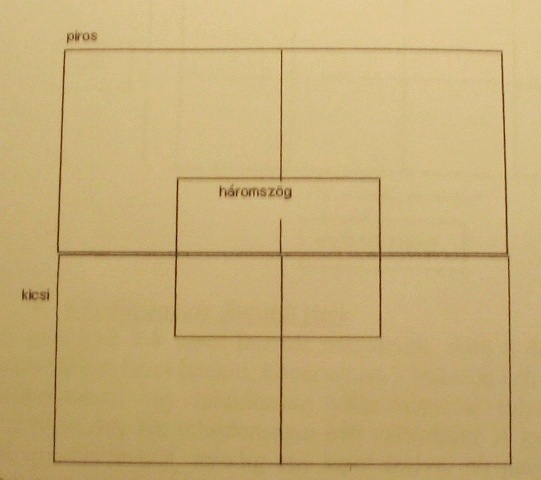
Válogatás mátrixba
Hol lesz a helye annak a lapnak, amely kicsi és háromszög alakú? Hovaa kerüljön, ami piros vagy kicsi vagy háromszög?
Melyik elem melyik részbe kerül?
Mely tulajdonságok jellemzik a közös részbe kerülő elemeket?
Játékok
A) Kapuőr játék
A gyerekek kapuőrt választanak. Minden gyerek jegyet vált, azaz választ egy lapot magának a készletből. A kapuőr kigondolja, de nem árulja el, hogy mely tulajdonságú lapokkal engedélyezi a belépést. A gyerekek egyenként odamennek az őrhöz, felmutatják a jegyüket. A kapuőr vagy engedélyt ad a belépésre vagy nem. Aki kitalálja, hogy mi a megfelelő belépőjegy, átveheti a kapuőr helyét.
B) Két kapuőr játék
A gyerekek előbb az első, majd a második őrnek is felmutatják jegyüket. Két tulajdonság egyidejű megléte kell ahhoz, hogy valaki bejusson a kapun. (Például a négyzet alakú lappal át lehet jutni az első kapun, de a másodikon csak a nagyok mehetnek át.)
Másik változata a játéknak, mikor a belépni vágyók vagy az egyik vagy a másik kapun léphetnek be. Például beléphet minden négyzet vagy vastag lap.
A kétféle játék nagyon jó segítséget nyújt az „és” és a „vagy” különbségének megértéséhez. Az első esetben két tulajdonság egyidejű megléte szükséges, a második esetben egy tulajdonság is elegendő a bejutáshoz.
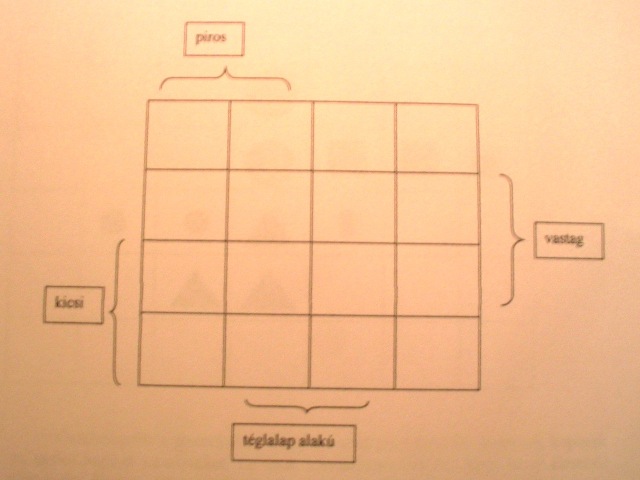
C) Két dimenziós dominó játék
A játékmező egyszerű kockás lap, akkora négyzetekkel, amelyekbe a Learning by logic egy-egy eleme kényelmesen elfér. A gyerekek 8-8 lapot húznak maguknak, mint a dominózásnál általában. A játékot a játékvezető indítja a középső mezőbe letett lappal. Vízszintesen egy tulajdonság változtatásával folytatható a sor, függőleges irányban már két tulajdonságot kell változtatni. A gyerekek felváltva foglalnak el egy-egy mezőt, mindig egy lapot letéve. Ha nem tudnak lapot letenni, kimaradnak, s húzniuk kell egy újabb lapot. Az győz, akinek hamarabb elfogynak a lapjai.
(Lehet úgy is játszani, ha már nagyon gyakorlottak a gyerekek a játékban, hogy zsákból húznak lapot. Ilyenkor megpróbálják kitapintani a megfelelő lapot. Jó tapasztalat, hogy a húzott lap színe ötféle is lehet.)