Az Alsós tanítói portálból

---

2007. december 9., 00:04 változat

Tartalomjegyzék 1 Megközelítés a rendszer felől 1.1 A tízezres számkör a számegyenesen 1.2 Számtáblázatokban 1.2.1 A számok írott és kimondott alakja

Megközelítés a rendszer felől

A számfogalomépítéshez a nagyobb számok körében választhatunk a korábbitól eltérő utat is. Korábban mindig valós számlálásokból, mérésekből indultunk ki. Most közelíthetünk a rendszer felől is.

A tízezres számkör a számegyenesen

Számegyenesen kiterjesztjük a rendszert, s ehhez gyűjtünk konkrét tapasztalatokat. Egyesével, tízesével, százasával lépegetünk, s figyeljük a kialakuló számokat. Amikor már sokat lépegettünk egyesével, tízesével ötvenesével százasával stb., akkor számegyenes-részleteken megjelölt számokat kerestetünk, majd felsoroltatunk számokat a számegyenes kijelölt (megvastagított) szakászáról.

A számegyenes egy-egy szakaszát kinagyítva kitalálós játékot játszunk. Az ezres szakaszról ráközelítünk előbb a százas, majd a tízes felosztású részletre, végül az egyes beosztású számegyenesen megjelölt számot kell megnevezni. (Tk. 64/32.)

Készítsünk számegyenest 0-tól 10000-ig. Ezresével akarjuk beosztani. Hány egyenlő részre osszuk fel a szalagot? 10 egyenlő részre

Hány táblára lesz szükség, hogy jelölhessük a számokat rajta?11 tábla kell

A gyerekek is elkészítik a saját számegyenesüket fonalból és gemkapcsokat használnak jelölésképpen. Ezalatt 3 tanulóval elkészítjük gumiszalag és gemkapcsok, valamint táblák felakasztgatásával a nagy demonstrációs számegyenest is.

Terítsék az asztalra a kész számegyenest! Olvassuk le róla a beosztásokat! Keressük meg egyes számok helyét! Tegyék a saját számegyenesükön a ceruzájuk hegyét oda, ahol szerintük az  5120, (2004, 1955, stb.) helye van!

Mutassák meg a nagy számegyenesen is! Melyik két ezres közé helyezted?

Megfigyeltetjük, hogy az egység nagysága nem befolyásolja a számok helyét a számegyenesen

 Van állandó helye a számoknak a számegyenesen? A gyerekek véleményének meghallgatása.

Figyeljék meg a változást! Megnyújtjuk a gumiszalagot.

Mi változott meg? A számok arrébb kerültek.

Hogyan változott a számok közötti távolság? Nagyobb lett.

Mitől lett nagyobb?A nyújtástól.

Hogyan változott az egység? Nagyobb lett.

Mi nem változott meg?

Nem változott a számok sorrendje.

Nem változott a számok egymáshoz való viszonya.

Mondjanak példát az osztályban arra, hogy a számegyenesen kisebb az egység, de az 5002 szám helye továbbra is az 5000 és a 6000 között van?(Saját számegyenesén láthatja, amit az előbb készített)</p>

Számtáblázatokban

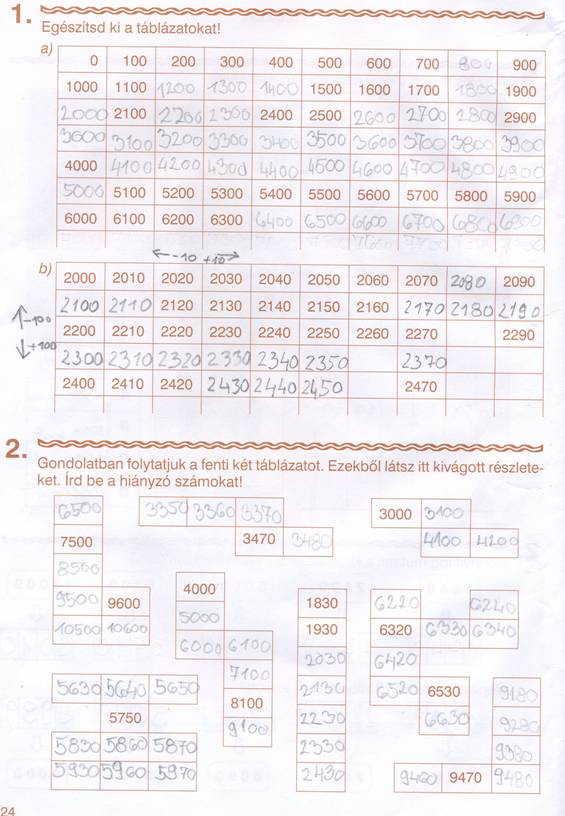
<p>Táblázatokban elrendezett számok között keressük a rendszert. Olyan táblázatot használunk, amely jól tükrözi a tízes számrendszert. Leolvassuk az egyes számokat, majd hiányzó számokat pótoltatunk. Megfigyeltetjük, milyen szabály szerint változnak a számok a különböző alakzatokban. (Lefelé ezresével növekszenek, jobbra százasával, balra százasával csökkennek, fölfelé ezresével csökkennek. (Munkafüzet 24/1.2.)</p>

<p> </p>

A számok írott és kimondott alakja

<p>A számok írott alakját könnyebb megfigyelni, s így könnyebb a rendszert felismerni az ismétlődő formai jegyekben. A számok kimondott alakjával nehezebben boldogul a kisgyermek, ezért külön foglalkozunk a hangos számlálásokkal is. Gondolkodunk azon, hogy meddig tartana ezerig elszámlálni. Ezalatt hányszor ejtjük ki az 1, 2, 3, … számneveket. Egyáltalában hány háromjegyű szám van? Hányszor mondjuk ki a száz, kétszáz, háromszáz szavakat miközben a számlálunk? Hány szám van 10000-ig? </p>

<p>Számok valóságtartalma</p>

<p>És még mindig a rendszer</p>

<p>A számegyenesen, táblázatokban való tájékozódás mellett igyekeznünk kell a számok valóságtartalmát is megvilágítani Darab- és mérőszámértelemben, valamint vásárlóérték szempontjából járjuk körül a témát.</p>

<p>Darabszámként a csoportosítva számlálás módszerét használva fénymásolópapír-csomagokat számlálunk le ötszázasával. Gemkapocs csomagokban lévő mennyiséget adunk meg, százasával csomagolt postai levélborítékok mennyiségét adjuk meg.  (Tankönyv1. 59/12)</p>

<p> </p>

<p>Gemkapcsokból láncot fűzünk. Tízezer kapcsot használunk mindkét lánchoz. Hány m hosszú lánc alakul ki? A tényleges felfűzésre nincs mód, ezért csak elkezdjük, majd áttérünk az okoskodásra.</p>

<p>3 és 5 cm-es kapcsokból váltakozva ismét láncot fűzünk. Milyen hosszú lesz így a lánc, ha összesen tízezer darabot használunk fel.</p>

<p>Izgalmas a mértékváltás kiokoskodása, de a kiszámítás módszereit is megvizsgálhatjuk. Kiszámítás a 3 cm tízezerszerezésével. Kiszámítás az 5 cm tízezerszeresének kiszámításával. Ezek egyszerűek.</p>

<p>- A váltott láncszemű (3cm, 5 cm, 3 cm, 5 cm…) lánc kiszámítási módszerei: 3 cm + 5cm= 8 - cm és ennek a tízezerszerese</p>

<p>- A 3m · 10000 és 5 cm · 10000 összeadása, majd megfelezése</p>

<p>- 3cm · 5000 + 5 cm · 5000 is vezethet eredményre</p>

<p>A feladat érdekessége komplexitásában rejlik. A darabszám nem kerül kirakásra, főleg a képzelet működik, ám az eredmény megérthető, belátható távolság. 300 m, 500 m, 400 m, ennyit a kisgyerek ki tud mérni az iskola udvarán vagy folyosóin is. Egy ilyen hosszú lánc elképzelése érzékelteti a darabszám számára hallatlan nagyságát.</p>

<p>Miből lehet az iskolában tízezer darab? A kérdés megindítja a gyerekek fantáziáját. Tankönyvekből – fogják mondani. Adatgyűjtéssel igazolunk. Hány osztály van? Hány gyerek jár átlagosan egy osztályba? Egy gyereknek hány tankönyve van? Más osztályokban is ennyi van? Átlag kialakítása következik– információforrásként a testvérekről tudnak beszámolni. Egy sor szorzás elvégzése után tudnak válaszolni a kérdésre. Lehet a könyvtárnak is? A pedagógusoknak is van? A feladat haszna nemcsak a számkör kiterjesztésében, az okoskodásban van (a számolási eljárások átvitelében a nagyobb számkörre), hanem növeli a gyerekek átlagos tájékozottságát, kiterjeszti érdeklődésüket a tágabb iskolai közösségre is.</p>

<p>Mérőszámként hosszúság- tömeg- terület- és időméréshez kapcsoljuk a tízezer nagyságának elképzelését.</p>

<p>A milliméterpapíron a négyzetmilliméterhez, négyzetcentiméterhez, négyzetdeciméterhez is kapcsolhatjuk a tízezret. Először leszámlálással kezdjük. Megállapítjuk, hogy a legkisebb négyzet oldalai 1 milliméter hosszúságúak. Ez egy mm2. Tíz kis négyzet egy keskeny oszlop, tíz ilyen oszlop száz négyzetmilliméter. Ha ezt is megmérjük, rájövünk, hogy pontosan 1 cm oldalú négyzetet kaptunk. Ez 1 cm2. Tíz darab ilyen négyzetcentiméter ezer négyzetmillimétert tartalmaz. Tízszer tíz ilyen tízezer négyzetcentiméter, s egyben 1 dm oldalú négyzetet tudtunk összerakni. Ezután körülkerítünk a milliméterpapíron tetszőleges nagyságú területeket, s ezeket próbáljuk darabszámként, illetve mérőszámként is kifejezni (Tankönyv 57 és 58/3.).</p>

<p>Kijelölt nagyságú milliméterpapírra rajzolt területeket adunk meg. Hány ezres, hány százas és hány tízes, illetve egyes egységből állnak ezek az alakzatok? Leltárt készíttetünk a gyerekekkel. A helyiérték-táblázatba számkártyákkal jegyeztetjük le az eredményt, majd a kapott számot kiolvassuk.</p>

<p>Megtippeltetjük, hogy milyen nehéz lehet 10 egyforintos. Mekkora lehet a tömege tízezer egyforintosnak? Következtetéssel dolgozunk.</p>

<p class=dvv>Megkérdezhetjük a gyerekektől:</p>

<p>Mit gondoltok, van az iskolában 10000 padlócsempe? Rövid vita után, amely főként az épület nagyságával, a járófelülete területével kapcsolatosan az általánosságok szintjén zajlik (nagy, hosszúak a folyosók, a mosdókban is van, van alagsor is, stb.) feladatul adhatjuk, hogy közelítő számlálást végezzenek. Ha nagy az épület, akkor csoportonként egy-egy szintet vizsgáljanak. Beszéljék meg, hogy milyen módszer a legcélravezetőbb, mert az egyesével leszámlálás nagyon unalmas. A következő módszereket fogják alkalmazni:</p>

<p>A terület darabolása négyzet vagy téglalap alakú részekre.</p>

<p>Sorok és oszlopok leszámlálása, szorzással területszámítás</p>

<p class=lista>Mintázat megfigyelése</p>

<p class=lista>Mintaegységek leszámlálása</p>

<p class=lista>Összeszorzással a használt csempék számának megállapítása</p>

<p class=lista>Szabálytalan alakú területeknél igen durva becslés alkotás</p>

<p class=lista>Részeredmények összeadása</p>

<p class=lista>Szintek számával való beszorzása</p>

<p>A tevékenység haszna:</p>

<p class=lista>Tapasztalatszerzés konkrét területméréssel kapcsolatban</p>

<p class=lista>Területszámítási eljárás kitalálása, végrehajtás</p>

<p class=lista>Ismerkedés a tízezres számkör számaival</p>

<p class=lista>Számolási eljárások kiterjesztése önállóan a nagyobb számkörbe</p>

<p class=lista>A csoportban végzett munka öröme</p>

<p class=lista>Ötletdömping (A csoportban biztos lesz valaki, aki megindítja a feladatmegoldáshoz szükséges gondolatsort.)</p>

<p class=lista>Kontroll a feladatvégzésben (a társak állandóan korrigálásra késztetnek)</p>

<p>A vásárlóérték megfigyelésére olyan gyűjtőmunkát végeztetünk, amelyből kiderül, hogy mit lehet venni ötezer, nyolcezer, stb., forintért. Ekkor beszélhetünk arról, hogy ugyanannak az árunak az ára nem minden üzletben egyforma. Mi ennek az oka? Hol érdemes vásárolni? Ismét a szükséges hétköznapi tájékozottságot növelhetjük.</p>

<p class=dvv>A tízes számrendszer és a tízezres számkör</p>

<p>A tízes számrendszer megismerésére, működésének megértésére nem csak a számfogalom épülése miatt van szükség. Elengedhetetlen a kétjegyűvel való szorzás és osztás értő elvégzéséhez is.</p>

<p>Játékpénzekkel végeztetünk kirakásokat, ahol szükséges, beváltásokkal.</p>

<p class=dvv>Kirakás, (váltás), leltár

<p>1.Helyiérték-táblázatban dolgozunk. Az egyes fiókokat pénztárfiókokként kezeljük. Megbeszéljük, hogy mindig minden címletet a helyére kell rakni. Kirakunk egy összeget, csupa egyesekkel, tízesekkel, százasokkal, ezresekkel, majd leltárt írunk úgy, hogy a pénzek helyett feljegyzést teszünk a fiókba emlékeztetőnek, hogy ennyi darab volt az egyes címletekből.  Végül kiolvassuk a számot.</p>

<p class=idezet>(1 ezres 6 százas 5 tízes 3 egyes)</p>

<p>2. Kirakunk egy összeget, majd menet közben beváltást is végzünk. Leltározunk, ahogy az előbb, majd kiolvassuk a születő számot. (2 ezres 3 százas 12 tízes 5 egyes)</p>

<p>Kerek összegeket fizettetünk ki csupa egyessel, csupa tízessel, csupa százassal, csupa ezressel. Például a 6000 hatezer egyessel, 600 tízessel, 60 százassal és 6 ezressel fizethető ki. Helyiérték-táblázatba is kirakjuk számkártyával. Így a gyerekek jól megfigyelhetik a balra mozgást.</p>

<p>Ezután beírjuk a helyiérték-táblázat fejlécébe a váltásokat mutató nyilakat a változással. Olvastatunk a táblázat fejlécéről. Megfigyeltetjük, hogy balra minden egyes lépéssel tízszerezünk, jobbra lépésenként tizedet veszünk.</p>

<p>Azt is megfigyeltetjük, hogy két lépés százszoros, illetve százada mennyiséghez vezet, attól függően, hogy balra vagy jobbra lépünk. Három lépés az ezerszerese, ezrede kapcsolatról beszél. Nem rejtjük véka alá, hogy a táblázat jobbra, az egyeseknél kisebb számok irányába is folytatódni fog.</p>

<p>Tízszerese, tizede</p>

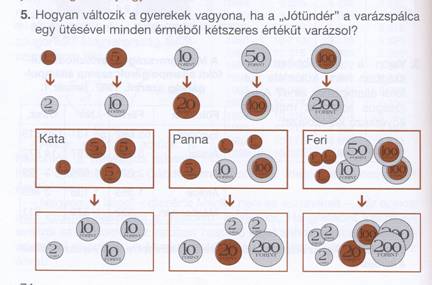
<p>Azt játsszuk a gyerekekkel, hogy mi lenne, ha egy jó tündér minden pénzérménket megérintené a varázspálcájával, s előbb megkétszereződne, megötszöröződne, végül megtízszereződne minden érme értéke. (Tankönyv 74-75.) </p>

<p>

</span>

Játékpénzzel eljátsszuk a cseréket, majd megállapítjuk, hogy Kata egyforintosa és 3 ötforintosa egy kétforintossá és 3 tízforintossá változna. Amikor a tízszerezést vizsgáljuk a helyiérték-táblázatunkban kirakjuk számkártyákkal az adott mennyiséget, majd a tízszerezés után balra egy hellyel betesszük a megfelelő helyre a számkártyákat. Le is rajzoljuk a füzetbe, és a változást

nyilakkal jelöljük. 5 --- 50

Megfigyeltetjük a jobbra mozgatásokat is. Kirakjuk helyiérték-táblázatba, lejegyezzük füzetbe a változást jelentő nyilakkal, majd leírjuk számtannyelven is

90 --- 9.

Megfigyeltetjük azt is, mi történik akkor, ha 2, 3 hellyel balra vagy jobbra toljuk el a számokat.

A mértékegységek használatát is a tízes számrendszerrel könnyítjük meg a gyerekeknek. Konkrét példákon mutatjuk meg, hogy jobban átlássák. Nemcsak a szabványos mértékegységeket írjuk be a táblázat fejlécében, hanem a közbülsőket is. Összegyűjtjük, feljegyezzük a kapcsolatokat is, majd elhelyezünk különféle mennyiségeket, s sokféleképpen kiolvastatjuk ezeket.

			1000000mm 100000cm 10000dm 1000m 1 km	100000mm 10000cm 1000dm 100 m	10000mm 1000cm 100dm 10m	1000mm 100cm 10dm 1m E	100mm 10cm 1dm sz	10mm 1 cm t	1 mm e
						1	2	4	2
						1 m	2 dm	4 cm	2 mm

1 m 242 mm,1 m 24 cm 2 m, 12 dm 42 mm, 1 m 2 dm 42 mm. Ilyeneket és hasonlókat olvastatunk le a táblázat segítségével. Addig, míg világos nem lesz, hogy egy mérőszám sokféle nevét mondja el. Az adott távolság standard.

Nyilakkal beírjuk a tízszeres, százszoros, ezerszeres, tízede, százada, ezrede kapcsolatokat is.

Kiolvastatjuk többféleképpen a táblázat segítségével. Kifejeztetjük cm-ben, deciméterben is a beírt mennyiségeket.

Ugyanígy járunk el a tömeg- és űrmértékek esetében is. Csak az ilyen gyakorlatok sokasága, és az ezek mellé rendelt konkrét mérések kapcsán kezdünk el átváltásokat végeztetni. Így nem esünk abba a hibába, hogy a kisgyerek megértés nélkül gépies módszereket használva „letakarok vagy hozzáírok két nullát” módszerrel vált át 1 dm-t mm-re vagy fordítva. Ezeket a szülők, nagyobb testvérek javasolják, de megértés nélkül csak verbális ismeretként rögződik átmeneti időre. A gyermek újra és újra elfelejti, s állandó szorongás forrása lehet, hogy nem érti az átváltást.

Ebben az időszakban tanítjuk meg a számnevek helyesírását is. Írjon le számokat hallás után.

Ilyenkor tanuljuk meg a római számokat is teljes körűen. Megfigyeltetjük, hogy bár van benne belső rendszer, de nem használ számrendszert, helyiérték-rendszert a római számírás. A római XXXVIII (38) ugyanannyi jelből áll, mint a CCCLIVI (366). Ha már begyakoroltuk, gyűjthetnek a gyerekek középületekről római számokat.

<pC. Neményi – Káldi: Matematika tankönyv és Munkafüzet 4. osztályosok számára</p> A laphoz nem tartoznak aloldalak.