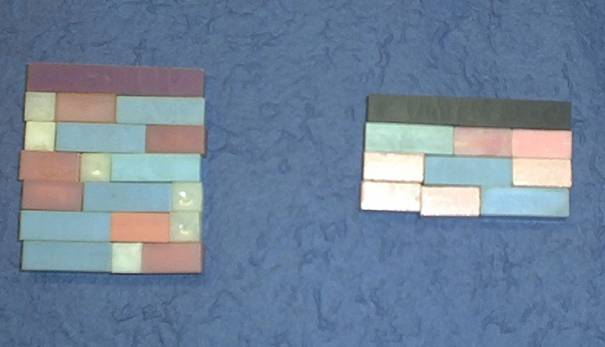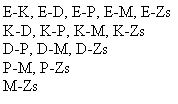Matematika/Tanterv/Gondolkodási műveletek/A kombinatorika az alsós tananyagban/Matematikai alapok csak felnőtteknek!
Az Alsós tanítói portálból
2007. december 9., 00:04 változat
A feltételek alapos megfigyeltetése, pontos megértése segít a matematikai tartalom feltárásában, egyben ez a megoldás kulcsa. A matematikai tartalom pontos megértése nélkül a tanító nem tud segítségére lenni a gyerekeknek a probléma meglátásában, megoldásában. Tisztázzuk hát a legfontosabbakat, de ne feledjük, a dőlt betűs magyarázat csak felnőtteknek szól!
Permutáció: adott elemeket minden lehetséges módon elrendezünk.
Ismétléses permutáció: az adott elemek között azonosak is vannak. A kétféle feladattípus más-más megoldási eljárást, más gondolkodásmódot igényel. A különbség kisgyerekek esetében csakis tevékenységgel érzékeltethető jól.
Szőnyegezzük a lila rudat fehér, rózsaszín és világoskék rudakkal.
Egy sorban mindhárom rudat fel kell használni! (6 megoldás lesz, mert a három rúd kétszer kerülhet első helyre. Ez ismétlés nélküli permutáció.
Szőnyegezzük a fekete színű rudat!
Két rózsaszín és egy világoskék rúd kerülhet egy sorba.
A megoldások száma csak három lesz. Ismétléses permutáció, mert a két rózsaszínt nem különböztetjük meg, hiába használtunk itt is három rudat egy sor kirakásához.
Ha kettes, hármas és négyes számjegyekből kell a kisgyereknek számokat összeállítania, más feladatot jelent, ha egy kártyát csak egyszer használhat fel, s megint mást, ha minden kártyából több is a rendelkezésére áll. a számkártyákból
Ha igazi számkártyákkal dolgozhat a kisgyerek, azonnal megérti a feltételeket, Ha a három számkártyát a kezébe fogva leteszi maga elé az egyiket, második helyre már csak a kezében maradó kettőből választhat, a harmadik helyre pedig a legutolsó kézben maradt kártyát kell letennie. Nem merülhet fel az ismétlés gondolata. Ezzel szemben a második feladatnál egy-egy számkártyából több is van a birtokában, tehát lehetnek olyan számok, amelyekben azonos számjegyek is előfordulnak.
Eleinte ha szóban vagy írásban kapja a feladatot a gyerek, nem tudja eldönteni, hogy lehetnek-e a számban egyforma számjegyek. Ha a feladatutasítás ezt nem zárja ki, természetesen lehetnek.
Mindig ügyeljünk a feladat korrekt, félreérthetetlen megfogalmazására, s vigyázzunk, hogy ne fogadjuk el a leszűkítő értelmezést!
Ciklikus permutáció: az elemek között nem jelölhető ki kitűntetett hely.
Egy kör minden negyedrészét más színűre színezzük piros, sárga, kék és zöld színnel. Hány különböző körlapunk lesz? A feladatot érdemes kivágott körlapokon megoldatni. Ha lenne első hely a negyedek között, akkor 24 megoldás lenne. Mivel ilyen nincs, a körlapok elforgatásával találhatunk egyformákat. Így csak pont a negyede, azaz 6 különböző körünk lesz.
Ábra: Animáció kiszínezett, színezés közben lévő, és színezés után megforgatott, egymásba úszó körökről
Variációk: különböző elemek közül valamennyit kiválogatunk és ezeket minden lehetséges módon sorba állítjuk. Itt is megkülönböztetünk ismétlés nélküli és ismétléses változatot.
Ismétlés nélküli:
Képezz a 4-es, 5-ös, és a 6-os számjegyekből kétjegyű számokat. Egy számjegy csak egyszer szerepelhet a számban
6 lehetőség van.
Míg, ha lehetővé válik az ismétlés,
Képezz a 4-es, 5-ös és a 6-os számjegyekből kétjegyű számokat. Mindegyikből sok kártyád van.
a lehetőségek száma 9, mert 3 olyan szám is keletkezik, amelyben a számjegyek azonosak:44, 55,és 66.
A megértésben a konkrét kirakás sokat segíthet.
A kombinációk feltételezik a permutáció és variáció számbavételét. Ismétléses és ismétlés nélküli esetek is megkülönböztethetőek.
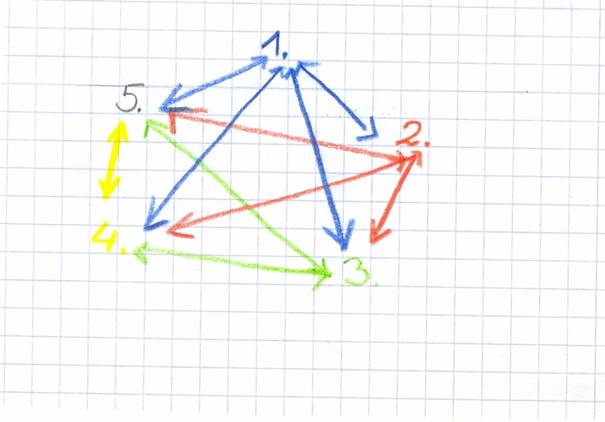
Hány kézfogás esik öt gyerek között?
Eljátszással kezdjük. Először 5 gyerek részvételével eljátsszuk! Engedjük a gyerekeket, hogy egy időben össze-vissza mindenki mindenkivel kezet fogjon. A gyerekek igényelni fogják a rendezett eljátszást. Így is eljátsszuk. Megoldásra jutunk.
Lejegyezzük a megoldást:
A probléma felvetése: Hány eset van, ha hatan koccintanak? Gondolkodjanak önállóan. Ezután tegyenek kísérletet a lejegyzésre. Betűkkel jelöljék a neveket. (Munkafüzet 51/1.)</span>
A megoldás:
Feltétlen megerősítésre szorul a gondolat, hogy E és K két személy, de köztük a kézfogás csak egy. E kezet fog K-val, de közben K kezet fog E-vel!
A lejegyzéskor kialakuló rendezett kép sokat segít majd a hasonló feladatokban. Segíti az estek gyors leszámolását is.
A tankönyvi és munkafüzeti feladatok C. Neményi-Wéber 3. osztályos, és C. Neményi-Káldi 4. osztályos Matematika tankönyvéből és munkafüzetéből valók.
A laphoz nem tartoznak aloldalak.