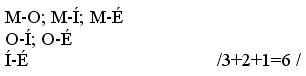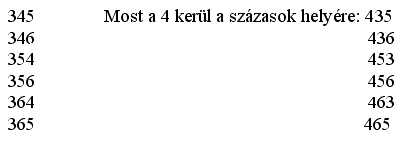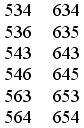Matematika/Tanterv/Gondolkodási műveletek/A kombinatorika az alsós tananyagban/A feladatmegoldást segítő módsezrek
Az Alsós tanítói portálból
2007. december 9., 00:04 változat
Tartalomjegyzék |
Eljátszások:
A sorrendek megfigyelése legkönnyebben eljátszással valósítható meg. Célunk még csak annyi lehet, hogy a gyerekek sokféle lehetőséget játsszanak el, s vegyék észre, ha újból ugyanolyan sorrendet képeznek, ami már korábban előfordult.
1. osztály
Kérjünk meg három kisgyereket, jöjjenek be többféleképpen az ajtón.
Sapkát, sálat, kesztyűt vegyenek fel, mindig más sorrendben.
Színes ceruzákat tegyenek a tolltartóba sokféleképpen.
Könyveket, füzeteket tegyenek egymásra más-más sorrendben.
2. osztály
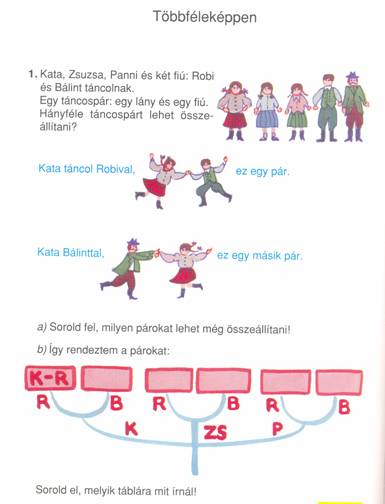
Táncospárok alakításának, kézfogások lehetséges variációinak számbavétele akkor válik maradandó tapasztalattá, ha el is játsszuk azokat. Jól illeszkedik egy tervezett absztrakciós folyamatba, ha egy-egy ilyen konkrét cselekvő tapasztalás után más kifejezését választjuk a megjelenítésnek, például kirakást vagy rajzot.
Kirakások:
Legoval, színes rúddal, gyöngyökkel, apró játékokkal, kártyákkal, számkártyákkal játszhatunk. A megoldásokat előbb szabadon kereshetik, majd rendezett formában is.
1. osztály
A kiválasztott kártyákat rakosgassák sokféleképpen a gyerekek. Egy-egy sorba rendezés után rajzolják le a sapkákat, hogy később ellenőrizhessék, előfordult-e már a kirakott sorrend.
2. osztály
Készítsenek szókártyákat a gyerekek, amit később sokféleképpen állíthatnak rendbe, akár más-más tartalmú feladat eszközeként.
Petinek hétfőn ezek az órái lesznek. Matek, Olvasás, Írás, Ének
Elfelejtette, milyen sorrendben követik egymást az órák. Segíts neki!
Készíts szókártyákat a tantárgyakról!
Állíts különböző sorrendeket!
A kirakásaidat jegyezd le!
Éva néni olvasást, írást, matekot, éneket tanít a 2. b-ben. Hétfőn csak két órája lesz a gyerekekkel.
Melyik két órája lesz?
Rakd ki a szókártyákkal!
A kirakásaidat jegyezd le!
Szócédulákkal is végezhetnek kirakásokat:
A logikai készlet lapjaival végzett kirakások rögzítését segíti az alábbi feladat
(Mf. 2. oszt. 48./1. feladat)
A feladat valószínűségi tapasztalatokhoz is juttat.
Párosítások:
Az ún. dominós feladatokban érdemes párosítással kipróbálni a lehetőségeket. Tisztáznunk kell, hogy legyen-e üres mező a készletben. Arról is fontos beszélnünk, hogy, amikor a „nap-hold” darabot készítjük, akkor egy megfordítással a „hold-nap” képet is leolvashatjuk róla.
Színezések:
Eleinte engedjük, hogy olyan sorrendben keressék a megoldást, ahogyan ötletszerűen eszükbe jut. Amikor az összes lehetséges megoldást keressük, mindent megjelenítünk a táblán. Vegyék észre, hogy ismétlődő esetek is vannak. Felébred a gyerekekben, vagy legalábbis a gyerekek egy részében, az igény a rendszerezett gyűjtésre. Sorrendeket kötünk ki: először például csak azokkal foglalkozzunk, amelyek piros színnel kezdődnek.
1. osztály
Tegyünk egy nem átlátszó zacskóba piros, kék, zöld és sárga cukrot. S próbáljuk meg kitalálni, hogy milyen színűeket fogunk kihúzni, ha kettőt, ha hármat fogunk kihúzni. Színes gyöngyökkel kirakhatják az egyes húzásokat, de p, k, s, z színű foltok rajzolásával le is jegyezhetjük a húzásokat. Ne keressük még az összes lehetséges megoldást, de állapítsuk meg, hogy még sokféle lehetőség van.
2. osztály
Különböző csíkozású zászlókat színezhetünk. Meg kell beszélnünk a gyerekekkel, hogy az egymás alatti csíkokat miért nem színezhetjük egyformára.
Oszlopos elrendezés:
Például a számképzéseknél jól használható. Gyakran az összes megoldás száma leolvasható róla előre, ha már kiderült, hány oszlop várható, s egy oszlopba hány különféle csoport kerül majd.
3. osztály
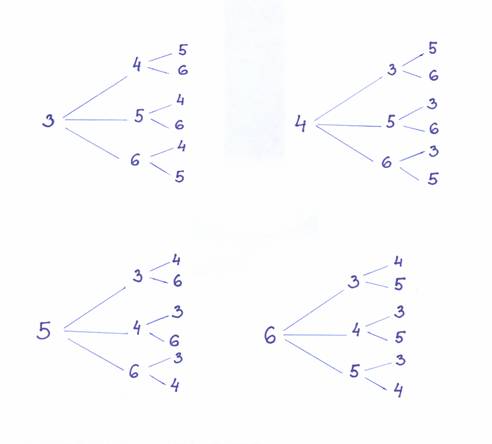
Írd fel az összes olyan háromjegyű számot, mely a hármas, négyes, ötös és hatos számjegyekből összeállítható! Egy számjegyet egy számban csak egyszer írhatsz le!
A gyerekekkel néhány spontán számalkotás után rátérhetünk a rendezett gyűjtésre. Kijelöljük a felhasználható helyiértékeket, s kiválasztunk egy számot a százas, majd a tízes helyre, végül a megmaradt számot letesszük az egyesek helyére:
Már most megjósolható, hogy 24 szám állítható elő ezekkel a feltételekkel, mert a hármast hat esetben tudtuk a százasok helyére tenni, a négyest is, s feltételezhető, hogy az ötös és hatos esetében is így lesz. 6·4ÿ=24. Ellenőrzésképpen folytatjuk a gyűjtést.
Természetesen a gyerekek által javasolt más rendszerben is gyűjthetők a számok.
Fadiagram:
Már első és második osztályban megismerkedtünk vele.
Zsuzsi babájának négyféle színes blúza és kétféle színes szoknyája van. Szeretné mindig másképpen felöltöztetni.
Hányféleképpen tudja felöltöztetni a babáját?
Rajzold le a „fa” segítségével az összeállításokat!
A Venn-diagrammal való ábrázolással nem most találkoznak először a gyerekek. A logikai készlet egy-egy részét már rakosgatták a 6, 8, 12 ágú fákra.
A feladat megoldását igazán jól előkészíteni akkor tudjuk, ha a táblánál előre kivágott babaruhákkal próbálgatjuk a különböző összeállításokat.
Tisztáznunk kell, hogy 6 féle színes ceruzára lesz szükségük a rajzolásnál.</span>
A gyerekek a rajzoláshoz kétféle 8 ágú fát kapnak.
Az első fának négy nagy ága van, megbeszéljük, hogy arra kerülnek majd a blúzok, hisz négyféle színűek. Minden nagy ágból két kis ág nő ki, ezek fölé rajzolhatják a két-kétféle szoknyát.
A másik fán két nagy ágból négy kis ág fölé rajzolnak úgy, hogy az azonos színű szoknyák és a négyféle színű blúzok látszanak egy-egy oldalon.
Le is írhatják számtannyelven:
Első fa: 2 · 4= 8
Második fa: 4 · 2= 8
Ez a szöveges feladat jól szolgálja a kombinatorikai témával kapcsolatos tennivalóinkat, de segít a szorzás műveletének egyik fontos tulajdonságáról, a felcserélhetőségről is tapasztalatot szerezni.
Harmadikban sokszor folyamodunk hozzá. Álló és fekvő helyzetben is használjuk. Külön gyakoroltatjuk a leolvasásokat is. Az előbb oszlopos elrendezésben felírt feladat megoldása fadiagrammal:
Táblázatos lejegyzés:
Ennek a fajta megoldásnak az előnye a jó átláthatóság, s hogy lehetővé teszi, hogy megsejtsük, hány csoport képezhető.
3. osztály
A gyerekek A, M, K és S betűk felhasználásával monogramokat írtak. Hányfélét tudtak felírni?
|
|
A |
M |
K |
S |
|
A |
AA |
AM |
AK |
AS |
|
M |
MA |
MM |
MK |
MS |
|
K |
KA |
KM |
KK |
KS |
|
S |
SA |
SM |
SK |
SS |
Útdiagram:
Ez is jól átlátható, lejárható. Célszerű eleinte az udvaron a földre rajzolni az utakat, s végiglépkedni rajtuk.
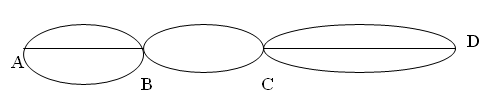
Hány különböző úton juthatunk el A faluból D faluba, ha ez az úthálózat?
Előnye, hogy szorzatalak leolvasásával megadható az eredmény (3·2·3=18).
Az adott feladathoz igyekszünk mindig a legcélszerűbb megjelenítési módot választani. Gyakran egyben a feladat megértésének feltétele a választott megjelenítési és megoldási mód. Ismertebb feladattípusnál egymás után többféleképpen is megoldhatjuk a feladatot, hogy összevethessék a gyerekek, melyik a kedvezőbb vagy éppen a nekik inkább tetsző.
C. Neményi-Sz. Oravecz Matematika Munkafüzet 4. melléklete</span>
Az elsős és másodikos feladatoka C. Neményi-Sz. Oravecz tankönyvekből és munkafüzetekből valók.
A laphoz nem tartoznak aloldalak.