Matematika/Tanterv/Geometria, mérés/Geometriai mennyiségek és mérésük
Az Alsós tanítói portálból
2007. december 9., 00:04 változat
A mérés az alsó tagozatban nem kötődik kizárólagosan a geometriához. Nagy hangsúllyal szerepel a számfogalomépítésben. Ezekről a számfogalomalakítás témakör tárgyalásánál szólunk. Most csak a geometriai mennyiségfogalmak formálásáról beszélünk. Geometriai mennyiségeken a hosszúságot, területet, térfogatot és a szöget értjük. A geometriai mennyiségfogalom formálásához hozzátartozik a mérés mint tényleges, gyakorlati tevékenység. A tananyag szétosztása az első négy évfolyamra kijelöli tennivalóinkat, s egyben a fokozatosságot is biztosítja.
Tartalomjegyzék |
A mérés mint tevékenység
A mérőszámokkal való ismerkedés közben valóságos mérésekre támaszkodva pontosítjuk a kisgyermek fogalmait a méréssel kapcsolatban. Tisztázzuk a különbséget az összemérés és megmérés között. A két fogalom kétféle tevékenységet takar. Csak akkor érti a gyerek, ha sokszor végzi mindkettőt. Összeméréskor viszonylatokra derül fény; ki magasabb, ki alacsonyabb, mi rövidebb, mi hosszabb, mennyivel nehezebb, könnyebb. De az összemérés önmagában nem vezet mérési eredményhez. Ha két tanulót egymás mellé állítunk, nem tudjuk megmondani, hogy ki hány cm magas. Ahhoz, hogy adathoz jussunk meg kell mérnünk őket. A mérés összehasonlítás. Azt állapítjuk meg vele, hogy a mérendő mennyiség hányszorosa a mértékegységnek. A pad szélessége ötszöröse a narancssárga rúdnak, mert a narancssárga rúdból öt kell a kirakáshoz. A gyermek kisaraszának négyszerese, a cm-nyi távolságnak 50-szerese.
Alkalmi és szabványos mértékegységek használata
A mindennapi életben gyakran találkozunk alkalmi mérőegységekkel. A süteménybe csipetnyi sót, öt kanál lisztet, egy bögre tejet teszünk, aztán ujjnyi vastagra nyújtjuk. Elmegyünk a szemközti boltba, ami csak tíz lépésre van tőlünk. A komódnak, amit meg akarunk venni, tíz arasznál rövidebbnek kell lennie, mert különben nem fér be az étkező sarkába. Máskor szükséges a szabvány egységgel végzett pontos mérés. Van olyan sütemény, amihez egy dekával sem tehetünk több lisztet vagy élesztőt az előírtnál, mert különben nem sikerül. Bútort is néha centiméterre pontosan kell választanunk, különben nem fér el a leendő helyén. Első osztályban gyakran mérünk, hisz a számfogalom-építés szerves része a mérőszámmal értelmezett szám. A hosszúság mérésekor a lépésekkel, araszokkal, zsinegekkel való méréseken kívül mérhetnek a gyerekek a színesrudakkal is.
Az űrtartalom mérésekor tejfölös poharakkal, orvosságos üvegekkel, gyűszűvel, üdítős üvegekkel biztosíthatjuk az alkalmi egységekkel való mérés eszközeit. Tömegméréshez jól használható az ún.vállfa-mérleg A súlyokat helyettesítheti az üveggolyó, az öt vagy –tízforintos érme, a gesztenye, stb.
Vállfa-mérleg
A kisgyerek csak akkor látja be a pontos mérés szükségességét, ha tapasztalatot szerez alkalmi mérésekről is. Tapasztalnia kell, hogy ő azért lépett kevesebbet, mint a padtársa, mikor a tanterem hosszát mérték, mert nagyobbakat lép nála. Színesrudakkal való méréskor később tovább építhető a gondolat a mértékegységekről: kétszer akkora rúdból fele annyi, négyszer akkora rúdból negyed annyi, stb. kell a hosszúság megméréséhez. Kisebb pohárból több kell, mint nagyobból, hogy a kancsót teletöltsük vízzel. Rizsszemből sokkal több kell, mint babszemből ugyanakkora pohár teletöltéséhez. Ezek a tapasztalatok nemcsak arról győznek meg, hogy egységesen megválasztott mértékkel kell mérnünk, hanem arról is, hogy kicsi egységből több, a nagyobb egységből kevesebb szükséges a méréskor.
Mérés adott pontossággal
A gyakorlati mérés sohasem lehet teljesen pontos. A gyerekek észreveszik, kifejezik, hogy az araszuknál kicsit nagyobb a könyv, a tanterem széltében kicsivel több, mint 12 lépés, a postairón néhány mm-rel hosszabb, mint valahány cm. Mindig fogadjuk el ezt az észrevételt, mert ebből következik majd a mérés pontosságának, illetve a szükséges pontosságnak a gondolata. Megtanuljuk megválasztani, és kifejezni azt is, hogy milyen pontosságú mérést végezünk.
Azt a tapasztalatot kell megszerezniük a gyerekeknek, hogy adott esetben a mérőeszköz megválasztása a saját döntésünk lehet. A választást az befolyásolja, hogy milyen pontosságra van szükségünk. Ennek megfelelően választjuk meg, hogy milyen mérőegységgel mérünk. Nemcsak a mérőeszköz megválasztását kell gyakoroltatnunk, hanem a mért érték leolvasásának módszerét is. Például fontos a mérést a 0 jelölésnél/beosztásnál kezdeni és a mért hosszúsághoz legközelebbi jelölést/beosztást leolvasni hosszúságméréskor. A kapott mérőszám a mért hosszúság adott egység pontosságú értéke.
Például: Ha a harmadikos kisgyermek a táskájára jellemző adatokra kíváncsi, elegendő a centiméteres pontosságú mérés. A ceruzájáról nem fontos azt lejegyeznie, hogy 10 cm és 2 mm hosszú. Elég, ha azt mondja, hogy ez megközelítőleg 10 cm.
A tankönyvét megmérheti deciméteres pontossággal: 2 dm lesz, centiméteres pontossággal 22 cm lesz. A milliméteres pontosságú mérésre pedig nincs szükség. Ugyanígy elfogadhatunk 5-6 szem almát 1 kilogrammnyinak akkor is, ha a tényleges tömege csak 97 dkg vagy éppen 102 dkg, de ha sütemény hozzávalóját mérjük, sokkal nagyobb pontosságra törekszünk. A gyógyszertárban a gyógyszerek összetevőinek mérésekor a legkisebb tévedés sem engedhető meg.
Gyűjtsenek a gyerekek példákat arra, amikor csak bizonyos pontosságú mérésre van szükség.
Hosszúságmérés
Első osztálytól kezdve gyakran mérünk, hisz a számfogalomépítés szerves része a mérőszámmal értelmezett szám. A hosszúság mérésekor a lépésekkel, araszokkal, zsinegekkel való méréseken kívül mérhetnek a gyerekek a színesrudakkal is. Az egység fogalmának tapasztalati alapjait kezdjük lefektetni. Fontos gondolat, hogy választott, megközelítőleg egyenlő nagyságú tárgyak alkalmasak a mérésre. Azt figyeltetjük meg, hogy adott távolság hány egységnek feletethető meg, hány egységgel rakható ki. Később bevezetjük a szabványos mértékegységekkel való mérést is. Itt a mérőegység állandó nagyságú. A sokszori ismételt mérésekkel arra törekszünk, hogy a kisgyereknek kifejlődjön az egységekkel kapcsolatos állandó képe. Ezért gyakran kérjük, hogy mutassák meg körülbelül mekkora 1 cm, 1 m, stb. Azonnal ellenőrizzük is az elképzelt hosszúságot konkrét méréssel, és korrigálunk. Újra megmutatjuk a szóban forgó távolságot. Majd az egység többszöröseit becsültetjük. Rajzoljon 10 cm, 50 cm, stb. hosszú vonalat, vágjon le a tanuló 20 cm hosszú papírcsíkot a pénztárszalagból! Mindig ellenőrizzük méréssel, hogyan sikerült megbecsülni a távolságot.
Tömegmérés
A tömegmérés tanításakor nincsen lehetőségünk a tömeg és a súly közötti finom különbségtétel megértetésére, mert ehhez olyan fizikai fogalmakat kellene megmagyaráznunk a kisgyereknek, amit nem érthet még meg. Megkülönböztetjük a szóhasználatban. Mi mindig tömegmérésről beszélünk, de egyébként nem foglalkozunk vele. A ki a nehezebb, mi a nehezebb kérdés feloldja a problémát.
Kezdetben a kisgyerek a két kinyújtott kezén való méricskéléssel szerez tapasztalatot. A nehezebb tárgy jobban húzza lefelé a karját, mint a könnyebb. A vállfa mérlegre akasztott két zacskó közül a nehezebb lejjebb van. Amikor a mérleg működését figyeltetjük meg, erre a tapasztalatra építünk.
Bőven teremtünk lehetőséget a kétkarú mérleggel való mérésre, azért, hogy a kisgyerek a mérés élményét átélje. A legtöbb kisgyereknek nincs alkalma otthon erre a tevékenységre. Ha mérnek is sütés közben, inkább digitális mérleget használnak a modern konyhában, s ez megnehezíti a mérés élményének átélését. A kétkarú mérleggel jól látható a mérés folyamata, a kiegyensúlyozódás, a mennyiségek lassankénti egyenlővé válása szemmel is nyomon követhető, miközben a mérleg serpenyőjébe rakosgatja a gyerek a súlyokat. Hasznos, ahogy latolgatja kisebb vagy nagyobb egység kell még, stb. A kétkarú mérleg egyensúlyban van, ha azonos tömeg van mindkét serpenyőjében. Ha az egyik serpenyőben növeljük a tömeget, nehezebb lesz, lejjebb kerül. A megfigyelteket a gyerek a padján kirakhatja, eljátszhatja. A papírserpenyők mozgatása és a színesrúd „súlyok” rakosgatása segíti abban, hogy megfigyelje, leutánozza, majd megértse a változásokat. Ez lesz az az emlékkép, amelyre majd a méréssel kapcsolatos feladatok megoldásánál támaszkodhat. Sőt a felsőbb osztályokban az egyenletek megoldása mérlegelv segítségével is csak úgy sikerülhet, ha átélt élmény emléke segíti.
Ismerkedjünk meg különféle mérlegeket! Mérhetjük a saját testük tömegét különböző mérlegekkel. Szoktunk kirándulni almáskertbe, ahol a nagy mérlegre, a mázsára, felállhatnak a gyerekek, s megmérhetik a testtömegüket. Fürdőszobai mérlegen is mérünk, és az orvosi szobában lévő személymérleget is bemutatjuk nekik. Érdekes számukra a levélmérleg és a patikamérleg is. Mérjük meg sokféle tárgy tömegét! Mérhetünk kedves játékszereket, hétköznapi csemegéket. De kíváncsiak lehetünk arra is, hogy a legkisebb súlyt, a grammot mivel egyensúlyozhatjuk ki. A mért adatokat aztán ábrázolhatjuk, feljegyezhetjük, s további leolvasásokat, értelmezéseket, összehasonlításokat végezhetünk.
Térfogatmérés
Teljesen szemléleti alapon történik. Amikor arra kíváncsi a gyerek, hogy a pohárba hány babszem fér, akkor inkább az űrtartalmat vizsgálja, amikor az a kérdés, hogy hány fehér kockából tud megépíteni egy adott építményt, térfogatot mér. Ennek megfelelően mindkét mérést végezzük. Alkalmat adunk rá, hogy különféle dobozokat töltögessen meg, s számlálja meg, hány egységet használt. Építgessen adott elemszámú testeket egyforma építőelemekből. Építsen csupa fehér kockából! Figyeljék meg, hogy sokfélét építettek, de az építmények közös tulajdonsága a térfogatuk, azaz, hogy adott számú kockát használtak hozzá.
Ha már sokat épített, próbálja megadni egy alma térfogatát. Vajon kb. hány fehér kockával lehet kirakni. A lereszelt almát mérőhengerbe rakva, megmérhetjük. Megpróbálhatjuk a kiszorított víz mennyiségét megmérni úgy, hogy az almát vízzel félig telt befőttes edénybe tesszük. Behelyezés előtt és után megjelöljük a víz magasságát. Másik edénybe letöltve a két jelölés közötti vízmennyiséget, megmutathatjuk, ennyi az alma térfogata. Szabványos mértékegységet még nem említünk, mert ez túl korai lenne. Kötődjön 1 liter víz mennyisége a literes edény hengeres, a zacskós tej hosszúkás vagy az 1 dm élhosszúságú kocka alakjához egyaránt. Sok megfigyelés után így fogja majd megérteni később a köbcentit, köbdecimétert.
Kerületmérés
Valójában hosszúságmérés. A kerületet, mint körüljárást fogjuk fel. Éppen ezért valóságos körüljárásokkal állapítjuk meg, mekkora az udvar kerülete, hány lépéssel járható körül. Hány lépéssel kerülhető meg a tanterem, hány citromsárga rúddal keríthető körül a pad? Különböző alakzatok hány négyzetoldalnyi vonallal keríthetők körbe a kockás lapon vagy füzetben. Hány centimétert vezettük a ceruzát, míg megrajzoltunk egy négyzetet? Az absztrakció útja világos, oda-vissza többször bejárjuk. Például kifeszítünk szögestáblán gumikarikát 12 egységnyi hosszan, rajzolunk olyan kerteket, amelyeknek 24 négyzetoldalnyi hosszúságú a kerülete, stb.
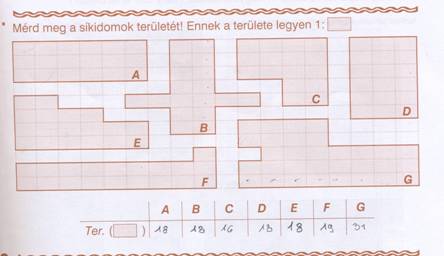
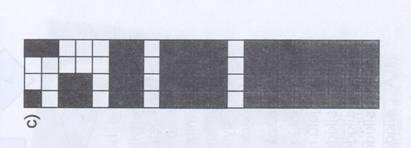
Területmérés
Míg a körbejárásról könnyű élményt adni, addig a lefedéssel mért területhez kevesebb élménye fűződik a kisgyereknek. Bár sokszor kipróbálta, hogy ráfér-e a falevél a rajzlapra, mégis az érzékszervi benyomás kevés. Tényleges összemérésekre van szüksége annak megállapításához, hogy két terítő közül melyik a nagyobb. Vannak esetek, amikor az alakbeli különbözőség miatt már az összemérés sem elegendő. Ilyenkor válik szükségessé az egységgel való mérés
Az egységgel való mérést úgy kezdjük, hogy egy nagy méretű lapon megfigyeltetjük, hogy ráfekvéssel, ráüléssel, ráállással hány gyerek foglalhat helyet. Az egység és a mérőszám közötti kapcsolat megértése után, további alkalmi egységekkel a mérünk. Kipróbáljuk a hézaggal való és a hézagmentes mérést. Megállapítjuk, hogy melyik vezet pontosabb eredményre. Sok alakalmi egységgel (babszem, kukoricaszem, körlap, háromszöglap, stb. Lásd parkettázás is) való mérés után rátérünk a négyzetekkel való mérésre. Ez még mindig nem a szabványegység. Haszna, hogy teljesen pontos az illeszkedés, s könnyen leszámolható. Gyorsítja a mérési eredmény létrejöttét, ha a sorok és oszlopok leszámlálása után szorzással dolgozunk. Azonban ne feledjük, hogy a fogalom, amit ki akarunk alakítani a lefedés és nem pedig egy gyors számolás. Ne feledjük, hogy területet csak területegységgel lehet mérni.
Például harmadik osztályban a feladatunk nem a négyzetcentiméterrel való ismerkedés, hanem a lefedéses területmérés fogalmának kialakítása.
A tényleges lefedések után hálókon való leszámlálás következik, majd hasznos, </span>ha csak kívül látható a háló , s úgy kell következtetni a lefedéshez használt lapocskákra.
Végül megfigyeltetjük, hogy fél egységekkel is lehet számolni – például háromszögek területének kiszámításakor.
Szögmérés
Amorf papírlapból egyenes hajtásával, majd annak egymásra fektetéssel történő felezésével derékszöget hozunk létre. Méréssel keresünk derékszögnél kisebb, nagyobb, ugyanakkora szögeket az osztály bútorain, ablakon, ajtón, tárgyakon, füzeten, könyvön. Nagyon pontosan tisztázzuk a szögtartomány fogalmát, anélkül, hogy ezt a szót kimondanánk. Állásban negyed fordulatokat téve, derékszögeket hozunk létre. Fordulunk ennél kisebbet, nagyobbat. Fehér papíron vagy homokban a cipőnk szépen kirajzolja a szögtartományt. Ezután színezéssel kerestetünk szögeket különböző sokszögeken. A kisgyerek ki fogja színezni nekünk a konkáv sokszögnél a külső szöget/szögeket. Engedjük, ne magyarázzunk! Vágjuk ki a sokszöget és kérdezzük meg, hogy az összes szöget beszínezte-e. Rögtön tisztázhatjuk, hogy az a szög kívül van, nem tartozik bele a sokszög oldalai által határolt területbe.
A szögmérővel való szögmérésre az első négy osztályban nincs szükség.
A laphoz nem tartoznak aloldalak.