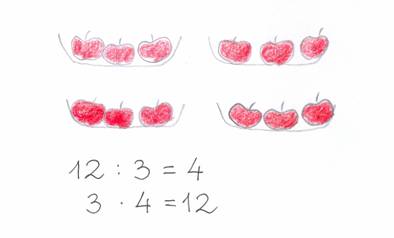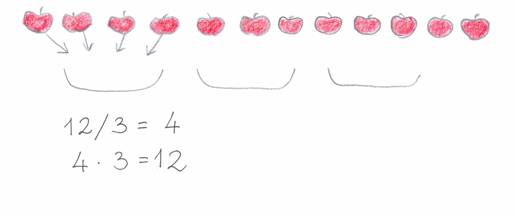Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Számfogalom - a számfogalom tapasztalati alapjai/Törtek
Az Alsós tanítói portálból
| (6 közbeeső változat nincs mutatva) | |||
| 93. sor: | 93. sor: | ||
== <h3>A témakör tanításának fokozatai</h3> == | == <h3>A témakör tanításának fokozatai</h3> == | ||
| - | '''I. Hétköznapi szóhasználat felőli közelítés''': alma, narancs | + | '''I. Hétköznapi szóhasználat felőli közelítés''': |
| - | csokoládé felezése, folyadékok széttöltögetése, fél kg, fél liter stb. | + | |
| + | alma, narancs, csokoládé felezése, folyadékok széttöltögetése, fél kg, fél liter stb. | ||
Gyűjtőmunkát kapcsolunk hozzá. Érdeklődjenek a gyerekek otthon, az | Gyűjtőmunkát kapcsolunk hozzá. Érdeklődjenek a gyerekek otthon, az | ||
élelmiszerboltban, mit lehet kapni fél kg-os, fél literes kiszerelésben. | élelmiszerboltban, mit lehet kapni fél kg-os, fél literes kiszerelésben. | ||
| 122. sor: | 123. sor: | ||
<p class=dvv>Egy rész neve?</p> | <p class=dvv>Egy rész neve?</p> | ||
| - | <p class=dvv>III. Mérések és egységtört: </p> | + | <p class=dvv>'''III. Mérések és egységtört''': </p> |
<p class=dvv>a, Színesrudak közül adott rudat több egyenlő rúddal rakunk ki. | <p class=dvv>a, Színesrudak közül adott rudat több egyenlő rúddal rakunk ki. | ||
| 252. sor: | 253. sor: | ||
számegyenesen való ábrázolása.</p> | számegyenesen való ábrázolása.</p> | ||
| - | < | + | <p>'''IV. Mennyiségek törtrészei'''</p> |
<p>Ebben az időszakban különösen fontos | <p>Ebben az időszakban különösen fontos | ||
| 298. sor: | 299. sor: | ||
a nagymutató által bejárt körrészre gondolunk, amikor a mutató a 6-os számra | a nagymutató által bejárt körrészre gondolunk, amikor a mutató a 6-os számra | ||
mutat. A fél óra nemcsak a 12-es és 6-os között telhet el. Sokat segít, ha | mutat. A fél óra nemcsak a 12-es és 6-os között telhet el. Sokat segít, ha | ||
| - | színes körcikkekkel is kirakjuk. Ugyanígy járunk el a negyedóra esetében is. Azt a helyzetet is megértetjük, hogy a negyedórát bármelyik időponttól kezdve számíthatjuk. [[Kép:Negyedóra.jpeg|left]]Amikor az egészhez való viszonyt jól érti, | + | színes körcikkekkel is kirakjuk. Ugyanígy járunk el a negyedóra esetében is. Azt a helyzetet is megértetjük, hogy a negyedórát bármelyik időponttól kezdve számíthatjuk. [[Kép:Negyedóra.jpeg|left]][[Kép:Negyedóra1.jpeg|left]]Amikor az egészhez való viszonyt jól érti, |
számolhatjuk percekkel is.</p> | számolhatjuk percekkel is.</p> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
<p>Az év a tizenkettes számrendszerhez kötődik. Ezért ezt külön | <p>Az év a tizenkettes számrendszerhez kötődik. Ezért ezt külön | ||
| 306. sor: | 380. sor: | ||
évszakokra a tananyagot.) </p> | évszakokra a tananyagot.) </p> | ||
| - | <p>V. Ismerkedés az egységtörtek többszöröseivel: Amikor már | + | <p>'''V. Ismerkedés az egységtörtek többszöröseivel''': Amikor már |
jól érti a kisgyerek az egységtörteket, áttérünk az egységtörtek | jól érti a kisgyerek az egységtörteket, áttérünk az egységtörtek | ||
többszöröseivel való ismerkedésre. Hasonló utat járhatunk be, ugyanazokat az | többszöröseivel való ismerkedésre. Hasonló utat járhatunk be, ugyanazokat az | ||
| 376. sor: | 450. sor: | ||
akkor van tapasztalat, amire támaszkodhatunk.</p> | akkor van tapasztalat, amire támaszkodhatunk.</p> | ||
| - | < | + | <p>'''VII. Törtek nagyságviszonyai''':</p> |
<p><span class=dvv>A törtszámok</span><span class=dvvChar>nagyságának | <p><span class=dvv>A törtszámok</span><span class=dvvChar>nagyságának | ||
| 404. sor: | 478. sor: | ||
megjelenítésével.</p> | megjelenítésével.</p> | ||
| - | <p> | + | <p>VIII. Műveletek:</p> |
<p>Amikor a gyerekek már sokoldalú | <p>Amikor a gyerekek már sokoldalú | ||
| 413. sor: | 487. sor: | ||
osztályban foglalkozunk.</p> | osztályban foglalkozunk.</p> | ||
| - | <p> | + | <p>IX. Az egész számok törtrészei témakörnél azt kell |
megértetnünk a gyerekekkel, hogy <span class=dvv>egy adott | megértetnünk a gyerekekkel, hogy <span class=dvv>egy adott | ||
számot </span>(12, 24, 90, 100, 1000, stb.) <span class=dvvChar> | számot </span>(12, 24, 90, 100, 1000, stb.) <span class=dvvChar> | ||
Aktuális változat
Tartalomjegyzék |
A törtek tanításának előkészítése 1-2 osztályban
Az első, második osztály matematika tantervi anyagában leghangsúlyozottabban a szám- és műveletfogalom alakítása áll.
A tört fogalmának előkészítése a szorzás, osztás 2. osztályban tanított anyagához kapcsolható leginkább. Az alsó tagozaton az osztást kétféle értelmezésben tanítjuk. Az egyik értelmezés az úgynevezett bennfoglalás, azt jelenti, hogy egyenlő elemszámú csoportokat készítünk, és azt kívánjuk megállapítani, hogy hány csoport kerül ki a rendelkezésre álló elemekből.
Azt mondjuk, 12 almából 3 almát 4 gyerek kap. 12-ben a 3 4-szer van meg. A bennfoglalásban az osztandó és az osztó ugyanolyan nemű (12 almában a 3 alma).
A másik értelmezés az úgynevezett egyenlő részekre osztás, röviden, részekre osztás, amiben adott, hogy hány egyenlő darabszámú csoportot kell létesíteni a rendelkezésünkre álló elemekből, de nem tudjuk, hogy egy-egy csoportba mennyi elem fog kerülni. Éppen ezt akarjuk megtudni. Lehet az az eljárás, hogy 4-4-4 darabot egyszerre a kezünkbe véve osztjuk szét egyesével a csoportokba (tányérokba) az elosztásra váró 12 almát.
Ez a módszer később elvezet az osztás egységes értelmezéséhez.
Azt mondjuk, hogy a 12 almát 4 egyenlő részre osztva 3 alma jut egy-egy tányérba, 12 osztva 4-gyel az 3 vagy 12 negyede az 3. A részekre osztásban az osztandó és a hányados lesz azonos nemű (12 alma/4=3 alma).
Ehhez a részekre osztáshoz fűzhetjük az egységtörtek értelmezését.
(Egységtört: olyan törtszám, amelynek számlálója 1.)
Sok-sok valóságos egyenlő részekre osztást végezve természetes helyzetben találkoznak a tanulók az 1 egész feldarabolásának lehetőségeivel.
A tört szám fogalmának alapozása 3-4. osztályban
A tört szám fogalma csak egyféle tapasztalati alapra épülhet, a mérésre.
A számérzet kialakulásához mindenféle mennyiség - hosszúság, terület, idő, tömeg, térfogat, űrtartalom - összemérését, mérését fel kell használni.
Csak konkrét tapasztalati értelmezésben haladunk:
megjelenítés,
leolvasás,
nagyság szerinti rendezés,
e számok sokféle neve,
s végül 1 egészre való kiegészítés.
4. osztályban bővül a tevékenység
a törtjelölés tanításával,
törtek a számegyenesen
és számok törtrészei témában.
Célunk, hogy 4. osztály végére önálló modellválasztással tudja a gyermek megjeleníteni az egységtörteket és azok többszöröseit. Képes legyen a törtek nagyság szerinti összehasonlítására.
A törtekkel kapcsolatos tevékenységet mindig valamely adott eszközzel és kijelölt egység használatával végezzük. Elképzelés útján, gondolati úton még a legjobb képességű tanulóban sem alakul ki a törtekkel kapcsolatos számérzet, számfogalom. Meg kell értenie a kisgyermeknek, hogy a tört a választott egységhez való viszonyt, arányt adja meg, hasonlóan a mérőszámhoz. Gyakorlatilag a fél/ketted lehet alma fele, dinnye fele, füzetlap vagy gyufaszál fele. A fél/ketted kifejezés nem egy adott állandó dolgot jelent, hanem az egészhez (egész alma, egész dinnye, .... stb.) való viszonyt.
A témakör tanításának fokozatai
I. Hétköznapi szóhasználat felőli közelítés:
alma, narancs, csokoládé felezése, folyadékok széttöltögetése, fél kg, fél liter stb. Gyűjtőmunkát kapcsolunk hozzá. Érdeklődjenek a gyerekek otthon, az élelmiszerboltban, mit lehet kapni fél kg-os, fél literes kiszerelésben. Búvárkodhatnak a szótárban is. Féleszű, félnótás, felibe-harmadába, feleség, stb. szavak jelentésének magyarázatával jutunk közelebb a kialakítandó fogalomhoz.
II. Megszámlálhatatlan mennyiségek (nagyjából) egyenlő részekre osztása
Sokat segít a megszámlálhatatlan mennyiségek (homok, liszt, rizs) felezése, harmadolása, negyedelése kupacalakítással. Tapasztalja meg, értse meg a tanuló, hogy az adott mennyiséget (egy egész kupac lisztet, homokot, rizst) egyenlő részekre osztottunk. 1 l víz negyedét állítjuk elő széttöltögetéssel. Rizs, homok vagy gyöngykupac negyedének kerestetése után almát, körlapot, fonalat és papírcsíkot negyedeltetünk. Az alábbi kérdésekre kerestetjük a választ:
Hogyan állítottad elő?
Hány részre osztottad?
Milyenek a részek egymáshoz képest?
Hány egyenlő rész van?
Egy rész neve?
III. Mérések és egységtört:
a, Színesrudak közül adott rudat több egyenlő rúddal rakunk ki. Megállapítjuk az egészhez való viszonyt, megnevezzük a részt.
Például a zöld rúd két lila rúddal rakható ki. Ha a zöld az 1 egész, akkor 1 lila rúd az 1 ketted. A zöld kirakható négy világoskékkel. Ha a zöld 1 egész, négy egyenlő darabból egy darab a negyedrész, azaz 1 negyed.
b, Adott területek harmadát, negyedét stb. színeztetjük vele négyzethálós lapon, tortaformán.
c, Általunk kiszínezett részterületről kell megállapítania, hogy mekkora részét színeztük ki az egésznek.
d, Papírcsík hajtogatásával, zsinór darabolásával állítjuk elő adott távolság kettedét, harmadát, stb.
Papírhajtogatás: Írólapot hajtogatunk, közben a megfigyeléseinket táblázatban rögzítjük. Megfigyeltetjük, leszámláltatjuk, hány rész keletkezetett. Elnevezzük a részeket. Azt is megszámláljuk, hány rész egy egész. Tippelünk a hajtás után, vajon hány rész lesz! A tippet számlálás kövesse!
|
Hajtások száma |
Keletkező részek száma |
Részek neve |
|
1 |
2 |
ketted |
|
2 |
4 |
negyed |
|
3 |
8 |
nyolcad |
|
4 |
16 |
tizenhatod |
|
5 |
|
|
A zsinórdarabolás alkalmas tevékenység annak bevezetésére, hogy adott szakasz miként osztható fel egyenlő részekre. Mi tartozik egy-egy részhez? Reprezentálható vele, ami a számegyenesen történik. Alkalmas eszköz az absztrakciós út végigjárására, míg konkrét tevékenységből – hajtogatás, csomóval való megjelölés -, elvont először szakaszon, majd a számegyenes 0 és 1 közötti szakaszán való ábrázolás nem lesz. Ebből a tevékenységből nő majd ki a törtek szakaszon, majd számegyenesen való ábrázolása.
IV. Mennyiségek törtrészei
Ebben az időszakban különösen fontos feladatunk a mértékegységek közötti tized-, század-, ezredkapcsolatok tisztázása, felismertetése. A hosszúság-, tömeg- és űrmértékek esetében konkrét tevékenységgel végezzük.
Ûrtartalom: 1 liter vizet 10 pohárkába töltünk. Egyenlő szétosztást végzünk. 1 pohár tartalma 1 tized liter víz. Ha ezt áttöltjük mérőedénybe, leolvashatjuk, hogy 1 tized liter az 1 dl-nek felel meg. Megkeressük a dl és cl közötti kapcsolatot, sőt a l és cl közti százada/százszorosa kapcsolatot is kiméregetjük.
Hosszúság: 1 méteres mérőszalagot hajtogatunk. Előállítjuk a tizedrészét. Leolvastatjuk dm-rel, cm-rel és mm-rel is a kapott mennyiséget. Megállapítjuk, hogy tizedrésze az 1 m-es távolságnak. A századrészt is megkeressük, de természetesen ilyen pontos hajtogatásra már nem vagyunk képesek. Segítségképpen a színes rúddal való kirakást használjuk. A méter ezredrésze a mm.
A tömeg mértékegységek törtrészeit is kerestetjük. Az 1 kg–os súllyal pontosan 4 margarinos csomagot tudunk kiegyensúlyozni. Fejezze ki egy margarin tömegét kilogrammban! 1 margarin negyed kg. 1 vaj ötöd kg, 1 kis vekni kenyér fél kg. Megfigyeltetjük, hogy egy kg-ot 10 db 10 dekás súlyra cserélhetünk be. 100 dekagrammal már a százada kapcsolatot találhatjuk meg. A narancssárga rúd 1 dkg-ot nyom. 100 db narancssárga rúddal kiegyensúlyozhatunk a mérlegen 1 kg-ot. 1 narancssárga rúd 10 fehér kocka tömegével egyenlő, így mód van a dkg-gramm kapcsolat felfedeztetésére is. Ezek időigényes feladatok, de a mértékváltást olyan fokon megkönnyítik, hogy megtakaríthatunk vele rengeteg értelem nélküli példamegoldást.
Az idő mértékegységeinek megfigyeltetését külön is elvégezzük, mert nem a tízes alapú számrendszerre épül. A negyed óra, fél óra, ötöd óra, stb. számbavétele esetén az egész 60 perc, ezt kell a gyereknek egyenlő részekre felosztania. Az idő ábrázolásával a kör azonos részekre felosztásában is gyakorlatot szerezhet. Ábrázolnunk kell a fél órát, de meg kell értetnünk, hogy a nagymutató által bejárt körrészre gondolunk, amikor a mutató a 6-os számra mutat. A fél óra nemcsak a 12-es és 6-os között telhet el. Sokat segít, ha színes körcikkekkel is kirakjuk. Ugyanígy járunk el a negyedóra esetében is. Azt a helyzetet is megértetjük, hogy a negyedórát bármelyik időponttól kezdve számíthatjuk.
Amikor az egészhez való viszonyt jól érti, számolhatjuk percekkel is.
Az év a tizenkettes számrendszerhez kötődik. Ezért ezt külön is vizsgáljuk. A tizenketted év, a negyedév mekkora időtartam? (Néhány naptáron is jól látható a negyedévekre tagolás. A nyelvtan tankönyv színekkel bontja évszakokra a tananyagot.)
V. Ismerkedés az egységtörtek többszöröseivel: Amikor már jól érti a kisgyerek az egységtörteket, áttérünk az egységtörtek többszöröseivel való ismerkedésre. Hasonló utat járhatunk be, ugyanazokat az eszközöket használjuk, mint az imént: homok, rizs, színesrudak távolságok, űrtartalom, időmérés, stb. konkrét méréseivel. Tapasztalja, értse meg a tanuló, hogy 1 egész egyenlő nagyságú részeiből többet neveztünk meg. Állítson elő 2 harmadot, 3 negyedet, 5 hatodot stb. Színezze sokféleképpen a 2 harmadot. Állapítsa meg, hogy mennyit ér a besatírozott rész. Ehhez először vissza kell következtetnie az egységtörtre, majd annak többszöröséhez jut.
Fontos, hogy nagyon sokféleképpen tapasztalja meg, hogy mekkora pl. 3 hatod. Színezze egy négyzethálós téglalapon sokféleképpen. Értse meg, hogy 3 hatodot színez akkor is, ha egymás melletti, de akkor is, ha egymás alatti négyzeteket satíroz be. Színezheti keresztben és össze-vissza is, csak az egészhez való viszony az állandó.
VI: A törtek sokféle neve: Miközben az egységtörtek többszöröseit vizsgáljuk, egyre sűrűbben teremtünk alkalmat arra, hogy a gyerekek észrevegyenek bizonyos hasonlóságokat. Például felfedezik, hogy ugyanannak az egésznek ugyanakkora a kettede, mint a 4 nyolcada, vagy a 2 negyede. Nem erőltetjük, de fokozatosan rávezetjük őket arra, hogy a törtszámoknak is van sokféle nevük. Sem a törtek egyszerűsítését, sem bővítését nem tanítjuk ezzel. Pusztán arra támaszkodunk, amit a gyerek tapasztal. Engedjük, hogy felfedezze magának a matematikát.
Megfigyeltetjük két mennyiség egymáshoz való arányát is. Hányszor
akkora? Mekkora része? Értse meg a kisgyerek, hogy az egység megválasztásának jelentősége
van. 
 </p>
</p>
Rajzolja meg a rész ismeretében az egészet. Ha ez egy ketted, mekkora az egész? Ha ez egy negyed, mekkora az egész?
Szöges táblán kifeszítünk 1 négyzetegységnyi területet befőttes gumival. Ez az 1 negyed. Mekkora lehet az 1 egész? Rá kell jönnie a kisgyereknek, hogy, bármilyen alakú négyszer akkora terület megfelel, de 4 egységnyi nagyságú legyen.
Érdekes feladat, ha különböző nagyságú és alakú papírlapokat teszünk a táblára, s azt mondjuk: Kértem a gyerekeket, hozzanak nekem egy negyed papírlapot, mert fel kell írnom valamit. Szolgálatkészen ezeket hozták a gyerekek:
Ki teljesítette jól a kérésem? Melyik gyerek érdemel dicséretet? Mindegyik negyed lapot hozott, mégsem egyformák a lapok. Hogy lehet ez?
Jó, ha a gyerekek rájönnek arra, mindegyik lap lehet negyed lap. Mindegyikhez elő tudjuk állítani a hozzá tartozó egész lapot. Ráméregetéssel bizonyítanak. Problémaként felmerülhet, hogy bizonyos irányban ráhelyezve negyede a kisebb lap a nagyobbnak, más irányban ez nem látható azonnal. Ennek az az oka, hogy a kisgyerek fejében, sokszor még a felnőtt fejében sem, alakult ki a terület mennyiségállandóságának fogalma. Átdarabolással lehet segíteni a megértést. Az átdarabolás nem alsós anyag, de nem fogadhatjuk el, hogy adott téglalapnak negyed része csak bizonyos helyzetben negyed része. Ahogy a 16-nak sem hol negyede a 4, hol pedig nem.
A témakör tanításánál felhasználjuk a tükrözésekkel kapcsolatban szerzett tapasztalatainkat is.
Gondolkodtató feladat, hogy állítson elő a tanuló ollóval egy egész szívecskét úgy, hogy csak a felét vágja ki, mégis az egész szív előtte lesz. Vagy negyed kört vághat, mégis egész kör legyen belőle. Rá kell jönnie, hogy a lap félbe, negyedbe hajtogatásával oldható meg a feladat. A vágásvonalak tengelyesen szimmetrikusak a hajtásélre, s így kihajtogatás után áll elő az egész forma. Vágathatunk fenyőfát, karácsonyi harangot, lepkét, virágot hasonlóképpen. Ha sokat nyírnak a technikaórákon, akkor van tapasztalat, amire támaszkodhatunk.
VII. Törtek nagyságviszonyai:
A törtszámoknagyságának összehasonlítása csak standard 1 egésszel történhet. Nem hasonlítható össze egy alma fele egy dinnye negyedével. Azonos területek különböző részeinek színezése, a színezett területek nagyságának összehasonlítása, összecsúsztatás, fedésbe hozás, összeforgatás segíthet abban, hogy a kisgyerek az „5 hatod nagyobb, mint a 3 negyed”-féle megállapításhoz eljusson.
Nagyon hasznos segédeszközünk a különböző színű papírkörökből álló, a sugár mentén bevágott törtkészlet, melyen fedésbe hozhatók az egyes törtek, s megfigyelhető egymáshoz képest a nagyságuk. Ugyancsak jó az írásvetítőre tehető színes dossziékból kivágott ilyen készlet. Átlátszósága segíti a tanítót a szemléltetésben.
A számegyenesen való eligazodással valójában, mint adott távolságot fogalmazzuk újra a törtszámot, de egyszersmind áttérünk a nagyságviszonyok elemzésére is. Nemcsak azt tudjuk leolvasni például a számegyenesről, hogy adott egységhez képest milyen távolság felel meg az egy harmadnak, hanem azt is, hogy a kettednél kisebb. Az effajta értelmezés lassan átcsúszik az adott távolság fogalmából abba, hogy a számegyenesen adott pontot feleltetünk meg egy törtszámnak Ezt az általánosítást nem siettetjük, mert a gyerekek egyéni haladási üteme nem egyforma. A többségnek ez a gondolat még túl korai. Õket segítjük, ha minden esetben, amikor a számegyenesen dolgozunk, végigsimíttatjuk velük a részt az elejétől. Főképpen a negyedik osztályban foglalkozunk a törtek számegyenesen való megjelenítésével.
VIII. Műveletek:
Amikor a gyerekek már sokoldalú tapasztalatot szereztek a törtek összehasonlításával a törtek nagyságviszonyairól, következhetnek a műveletek. Az alsó tagozaton csak az egy egészre való kiegészítésre szorítkozunk, s csakis eszközzel dolgozunk, hogy a kisgyerek minden esetben konkrét tapasztalatot szerezhessen. A témával főleg 4. osztályban foglalkozunk.
IX. Az egész számok törtrészei témakörnél azt kell megértetnünk a gyerekekkel, hogy egy adott számot (12, 24, 90, 100, 1000, stb.) egy egészként kezelünk, s azt egyenlően daraboljuk. Így jutunk a részekhez, s ezek többszöröseihez. Maguk a törtrészek ilyenkor egész számok. (Az alsó tagozaton csak egész számra vezető eseteket vizsgálunk. Néha utalunk arra, hogy másmilyen is van. Ez csak könnyen belátható esetben fordulhat elő. Pl. Az 5 kettede a két és fél. Még a leírás sem számmal, hanem betűkkel történik.) Ha eleget színeztünk négyzethálós papíron törtrészeket, a megfelelő előkészítés megtörtént, mert a gyerekek kiszámolgatták, hogy 12 vagy 24 négyzet negyede 3 vagy 6 négyzet, s ennek megfelelően színeztek. Most ide nyúlunk vissza. Mennyi a 60 negyede, harmada, stb.? Mennyi a 60 2 harmada, 3 negyede?
Később adott rész ismeretében visszakövetkeztetünk az egészre. „Egy szám harmada 20. Mennyi az egész?” típusú feladatokat oldunk meg.
VIII. Szöveges feladatokkal integrálhatjuk a törtekben való jártasságunkat a többi matematikai ismeretek közé
Egyszerűbb szöveges feladatokkal kezdjük: „Miki a zsebpénze valahanyad részét csokira költi” típusúakkal. Fontos, hogy megtanítsuk a gyerekeket az ilyen feladatok ábrázolására.
Receptekben megadott mennyiségeket felezhetünk, harmadolhatunk, negyedelhetünk. Szerencsés, ha nem csak szabvány mértékegységekkel megadottak vannak közöttük. Ne csak 24 dkg porcukor, 2 l tej és 48 dkg liszt negyedét számítsák ki, hanem gondolkodjanak azon is, hogy mennyi egy evőkanál őrölt fahéj negyede! Adjunk lehetőséget arra is, hogy a valóságban szerezhessen erről tapasztalatot!
Tyúkanyó egész nap kapirgált. Jutalma az elvégzett munkáért 1000 búzaszem fele, annak ötöde, annak fele, annak ötöde, annak fele, annak ötöde. Hány szem búzaszem Tyúkanyó jutalma?
A feladat megbeszélésekor be tudjuk mutatni hajtogatással a részek nagyságának drámai csökkenését.
Három aranyásó, Jack, Joe és Bill munkájuk végeztével összeültek, hogy az előzetes megállapodásnak megfelelően megosztozzanak a kincsen. Az arany felét Jack-nek ígérték, hiszen ő ismerte a lelőhelyet, a harmada Joe-t illeti, mert ő hozta a szerszámokat, a negyede Billé, mert munkájával segített. Jack hamar lemérte az arany felét, majd elsietett. Joe és Bill csúnyán összeveszett. Vajon miért?
Egy egyszerű rajzon hamar megértik a gyerekek, hogy 1/2+1/3+1/4 > 1
A törtjelölés bevezetése
A negyedik osztályban, amikor már a kisgyereknek terhes a hossza-dalmas leírás, akkor tanítjuk meg a törtszámok leírását. Rajzzal, hajtogatással keletkeztetjük a törtszámot, majd művelettel is leírjuk, s végül bemutatjuk a hozzá tartozó számot.
Az 1 negyed egy egész lap 4 egyenlő részre való osztásával keletkezett, azaz 1/4. Ezt így írjuk le törtszámmal:
a nevező
és a törtvonal kifejezéseket elemi szinten értelmezzük.
A nevező azt mutatja meg, hogy mekkora (hányad) részeket hoztunk létre. A számláló pedig azt, hogy hány ilyen rész van.
Tisztázzuk a gyerekekkel, hogy amikor azt mondjuk, tört, csak az ilyen alakban felírt számokra gondolunk. Közöttük azonban nemcsak törtszámok vannak, hanem tört alakban felírt egész számok is.
Gyakorlatképpen törtszámokat diktálunk. Írják le, karikázzák be közöttük az egész számokat. Beszéljük meg. Bizonyítsanak bármely alkalmas modellel.
Ezután újra olyan egyszerű feladatokkal folytatjuk a munkát, amelyek tevékenységet vagy rajzot igényelnek. Eközben a törtszám írását, olvasását, értelmezését, megjelenítését gyakoroltatjuk.
A laphoz nem tartoznak aloldalak.