Matematika/Tanterv/Számtan, algebra, sorozatok, függvények/Számfogalom - a számfogalom tapasztalati alapjai/A számkör, a számkörbővítés/Számfogalom az 1. osztályban
Az Alsós tanítói portálból
| (15 közbeeső változat nincs mutatva) | |||
| 87. sor: | 87. sor: | ||
<p>[[Image:cikk_22_image005.jpg]]</p> | <p>[[Image:cikk_22_image005.jpg]]</p> | ||
| + | |||
| + | '''A számok [[bontás]]a''' | ||
<p>A számok bontott alakja jól látható a képen. Ahogy | <p>A számok bontott alakja jól látható a képen. Ahogy | ||
válogatásokat végzünk (homokozó, labdázó, mászókázó gyerekek, fiúk-lányok, | válogatásokat végzünk (homokozó, labdázó, mászókázó gyerekek, fiúk-lányok, | ||
| - | stb.), természetessé válnak a nyolc <span class=dvv>összegalakjai</span>. | + | stb.), természetessé válnak a nyolc <span class=dvv>[[összegalakjai]]</span>. |
Fontos a leolvasásokat azzal a tudattal irányítanunk, hogy ezek a leolvasások <span class=dvv> | Fontos a leolvasásokat azzal a tudattal irányítanunk, hogy ezek a leolvasások <span class=dvv> | ||
nem matematikai műveletek</span>(összeadások)</p> | nem matematikai műveletek</span>(összeadások)</p> | ||
| 135. sor: | 137. sor: | ||
| - | *'''Probléma felvetése''': Pár vagy darab? | + | *'''Probléma felvetése''': Pár vagy darab? 10 kesztyű vagy 5 kesztyű van- e a kezemben? |
| - | ''Csak felnőtteknek! Összetartozó 2 darab alkot egy egységet, ezt nevezzük párnak.'' | + | ''Csak felnőtteknek! '''Összetartozó 2 darab alkot egy egységet, ezt nevezzük párnak'''.'' |
| - | *'''Tapasztalatgyűjtés:''' Párok, darabok számlása, számbavétele tárgyi tevékenységgel, a körülöttünk lévő | + | *'''Tapasztalatgyűjtés:''' Párok, darabok számlása, számbavétele tárgyi tevékenységgel, a körülöttünk lévő tárgyakkal. |
| - | + | Minden gyerek kap egy kis nejlonzacskót, amiben tárgyak vannak. Feladatuk, először, hogy rendezzék párba a tárgyakat. Majd a tanító kérdésére beszámolnak róla, hány darab, illetve hány pár tárgy van náluk. | |
Rendezetten felkerülnek a zacskók (mágnessel) a táblára. | Rendezetten felkerülnek a zacskók (mágnessel) a táblára. | ||
| + | |||
| + | [[Kép:fülbevaló.jpeg|left]][[Kép:babacipő.jpeg|left]] | ||
| + | |||
| + | |||
| + | játékcipők (Barbie készletből) | ||
| + | |||
| + | játék sportszerek (síbot, görkorcsolya, sítalp) | ||
| + | |||
| + | legóautók kerekei | ||
| + | |||
| + | hajgumik, csatok | ||
| + | |||
| + | fülbevalók | ||
| + | |||
| + | zoknik | ||
| + | |||
| + | kesztyűk | ||
| + | |||
| + | memóriakártyákból néhány lap | ||
| + | |||
| + | Fekete Péter kártyakészletből néhány lap | ||
| + | |||
| + | harisnyazoknik | ||
| + | |||
| + | |||
| + | *'''Párok és darabok előállítása:''' | ||
| + | |||
| + | Kétféle feladatot kapnak a gyerekeke: az egyik oszlopban ülők korongból és gyufaszálból 3 pár cseresznye kirakását, a másik oszlopban ülők 6 darab cseresznye kirakását. Ezután következik a két kirakás összehasonlítása a jelekkel. | ||
| + | |||
| + | *'''Képolvasások''': csomagolópapírról (bébicipők) | ||
| + | |||
| + | *'''Feladatmegoldások ''' | ||
| + | |||
| + | A Munkafüzet 41. oldalának feladatait oldják meg a gyerekek közös megbeszélés alapján önállóan. Majd páros munkában végzett ellenőrzés következik. | ||
| + | |||
| + | *'''Szorgalmi és házi feladat''' lehet „pár” gyűjtése rajzzal | ||
| + | |||
| + | *Időtől függően párképzésen alapuló kártyajátékkal zárhatjuk az órát. Memóriajátékokkal, Pőttyöskártyával vagy az Autóskártya készlettel játszhatnak a gyerekek. | ||
<h3>Számtulajdonságok</h3> | <h3>Számtulajdonságok</h3> | ||
Aktuális változat
A számfogalom előkészítése a tárgyak, dolgok tulajdonságainak megfigyeltetésével, szétválogatásokkal, összehasonlításokkal kezdődik már az óvodás életkorban. Az első osztályos kisgyerekek különböző szintű tapasztalati háttérrel kerülnek az iskolába, ezért rendkívül fontos, hogy képességeikről, ismereteikről a tanítók tudomást szerezzenek. Az első osztályos munka többek között ezért kezdődik egy rugalmasan kezelt (3-4 hét) előkészítő időszakkal.
Az előkészítő időszak célja a tanulók megismerésén túl, még a taneszközök megismertetése a gyerekek ismereteinek megközelítőleg egy szintre hozása, és a számfogalom előkészítése.
A számfogalom kialakításához nélkülözhetetlen szétválogatásokról, a tárgyak, dolgok megfigyelése alapján történő igaz, téves állítások kifejezéséről, sorbarendezésekről, szabályjátékokról más fejezetekben, elsősorban a Halmazok, logika témakörben írunk.
A természetes szám fogalma párhuzamosan két tapasztalati alapon épül: egyfelől darabszámként (tárgyak, meg- és leszámlálása), másfelől mérőszám (lelépések, kitöltések, lefedések, stb.) tartalommal. A fogalomépítés első lépése különböző érzékszervi benyomások szerzése például a több-kevesebb, az alacsonyabb-magasabb, a kisebb-nagyobb, a rövidebb-hosszabb, a szélesebb-keskenyebb, a kevesebb fér bele - több fér bele, a rövidebb ideig tart - hosszabb ideig tart viszonylatokról. Ha már a becslésszerű érzékszervi összehasonlítással a döntés lehetetlenné válik, akkor objektív módszert és eszközt alakítunk a fenti viszonyok megítélésére. A darabszámnál ez kölcsönösen egyértelmű megfeleltetéssel, párosítással történik. Így dönthető el, hogy valami több vagy kevesebb vagy ugyanannyi. A mérőszámnál valamilyen alkalmi mérőeszközt, mérőegységet(rúd, babszem, fonal, pénzérme, tejfölöspohár, stb.) használunk.
A több-kevesebb, kisebb-nagyobb, stb., valamint az ugyanannyi, ugyanakkora, stb. relációk jelölésére használt jeleket isekkor érdemes bevezetni.
A < ; > ; = jeleket a kisgyerekek mindig konkrét értelemben használják. Ezért a megnevezésük sem lehet általános. A 3 narancs több mint a 2 alma, a kosárban ugyanannyi a szilva mint a tálban, a hat meg kettő ugyanannyi mint a nyolc.
A számfogalmat az ugyanannyi relációhoz kötjük. A négy lépés, a négy taps, a négy korty üdítő, a kisautó négy kereke (elöl kettő, hátul kettő, azaz 2+2), a négy évszak , a négy szem cseresznye, a Kati szó négy betűje, a kabátomról az egy hiányzó, de még négy meglévő gomb (5-1), mind-mind a négyről szólnak. Ezekben az esetekben a lépés, a taps, a korty, stb. közös tulajdonsága, hogy mindegyikből négy van. A négy jele a 4-es szám. Nincs az a tankönyvi vagy munkafüzeti feladat, amelyik helyettesítheti, pótolhatja a valódi, több érzékszerv bevonásával történő cselekvő tapasztalatszerzést.
Jelenítsék meg a halmazok számosságát sokféleképpen eljátszásokkal, kirakásokkal, gyűjtésekkel, később rajzokkal, jelekkel. A számok írását elkezdhetjük, de akár késleltethetjük is.
Tartalomjegyzék |
Tanulói kirakás
Tanulói gyűjtések
Gyűjtés a kettőről
Gyűjtés a háromról
Gyűjtés a hatról
A számok sokféle alakja, sokféle neve
Már az ugyanannyik összeválogatásakor, összekeresésekor tapasztalhatják a gyerekek, hogy egy-egy szám többféle elrendezésben, alakban jelenik meg. (Tankönyv(1) 25. oldal)
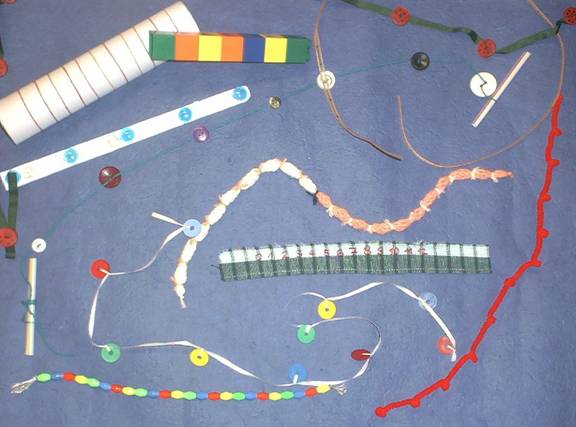
A számok bontása
A számok bontott alakja jól látható a képen. Ahogy válogatásokat végzünk (homokozó, labdázó, mászókázó gyerekek, fiúk-lányok, stb.), természetessé válnak a nyolc összegalakjai. Fontos a leolvasásokat azzal a tudattal irányítanunk, hogy ezek a leolvasások nem matematikai műveletek(összeadások)
A különbségalakok is gyakran fedezhetők fel környezetünkben. Legtermészetesebb módon úgy, ha valamilyen hiányt észlelünk. Például a nyolcágú fogason csak ötön látható sapka (8-3), egy levél vitaminon hét ép és három üres, feltépett hely van
(10-3), egy hatos tojástartóban öt tojás van (6-1)
Ahogy az összegalakban nem az összeadásra, ugyanúgy a különbségalakban nem a kivonásra gondolunk.
Számok helye a számvonalakon, számegyeneseken, számszomszédok
A kisgyerek számára a számegyenest is konkréttá lehet tenni, ha megengedjük, hogy létrán vagy lépcsőn vagy a földre ragasztott papírcsíkon le-föl, oda-vissza lépkedjen. A legjobb tapasztalat, ha a kisgyerek maga állít elő különféle számegyeneseket.
Természetesen a számegyenesen való lépkedést megelőzi a sorszámokkal való foglalkozás.
Ha házakat is rakunk az általunk készített számvonalra, és azokat számozzuk is, könnyen szemléletessé tehetjük a számszomszédok fogalmát.
Pár és darab fogalmának kialakítása
Vázlat
- Motiváció, ráhangolódás az órára párkereső játékkal:
A gyerekek húznak egy dobozból egy-egy darab kesztyűt, illetve zoknit, majd megkeresik azt a gyereket, akinél a pár másik fele van. A „zoknisok” és a „kesztyűsök” versenyeznek, kik találják meg egymást hamarabb. A játékban az egész osztály részt vehet.
- Probléma felvetése: Pár vagy darab? 10 kesztyű vagy 5 kesztyű van- e a kezemben?
Csak felnőtteknek! Összetartozó 2 darab alkot egy egységet, ezt nevezzük párnak.
- Tapasztalatgyűjtés: Párok, darabok számlása, számbavétele tárgyi tevékenységgel, a körülöttünk lévő tárgyakkal.
Minden gyerek kap egy kis nejlonzacskót, amiben tárgyak vannak. Feladatuk, először, hogy rendezzék párba a tárgyakat. Majd a tanító kérdésére beszámolnak róla, hány darab, illetve hány pár tárgy van náluk. Rendezetten felkerülnek a zacskók (mágnessel) a táblára.
játékcipők (Barbie készletből)
játék sportszerek (síbot, görkorcsolya, sítalp)
legóautók kerekei
hajgumik, csatok
fülbevalók
zoknik
kesztyűk
memóriakártyákból néhány lap
Fekete Péter kártyakészletből néhány lap
harisnyazoknik
- Párok és darabok előállítása:
Kétféle feladatot kapnak a gyerekeke: az egyik oszlopban ülők korongból és gyufaszálból 3 pár cseresznye kirakását, a másik oszlopban ülők 6 darab cseresznye kirakását. Ezután következik a két kirakás összehasonlítása a jelekkel.
- Képolvasások: csomagolópapírról (bébicipők)
- Feladatmegoldások
A Munkafüzet 41. oldalának feladatait oldják meg a gyerekek közös megbeszélés alapján önállóan. Majd páros munkában végzett ellenőrzés következik.
- Szorgalmi és házi feladat lehet „pár” gyűjtése rajzzal
- Időtől függően párképzésen alapuló kártyajátékkal zárhatjuk az órát. Memóriajátékokkal, Pőttyöskártyával vagy az Autóskártya készlettel játszhatnak a gyerekek.
Számtulajdonságok
A számfogalom kialakításához elengedhetetlen a számok tulajdonságainak megtapasztalása, megismerése. Gondolunk itt a számok nagyságára, oszthatóságára, a számok jegyeire, kirakhatóságukra bizonyos alakzatokban, a számok egymáshoz való viszonyára. Ezekről külön fejezetben szólunk. A számok tulajdonságainak megismerése már az első osztályban nagy hangsúllyal fordul elő. Természetesen, ahogy a későbbi osztályokban bővül a számkör, úgy terjesztjük ki a számtulajdonságokat a nagyobb számokra is. Fontos tudnunk, hogy a számok számrendszeres alakja nem lehet még tananyag az első osztályban, hiszen még csak a húszas számkörben dolgozunk.
C.Neményi-Sz.Oravecz: Matematika tankönyv 1. osztályosok számára I-II.
A laphoz nem tartoznak aloldalak.