Kreativitás

Az Alsós tanítói portálból

(Változatok közti eltérés)
(→Gazdagító játékok)
Aktuális változat (2008. március 26., 18:49) (szerkesztés) (visszavonás)
(→Gazdagító játékok)
 
(21 közbeeső változat nincs mutatva)
1. sor: 1. sor:
== A kreativitás alkotóképesség ==
== A kreativitás alkotóképesség ==
Az alkotóképes ember tapasztalatait, meglévő tudását úgy tudja átrendezni, hogy újszerű problémát is meg tudjon oldani.
Az alkotóképes ember tapasztalatait, meglévő tudását úgy tudja átrendezni, hogy újszerű problémát is meg tudjon oldani.
 +
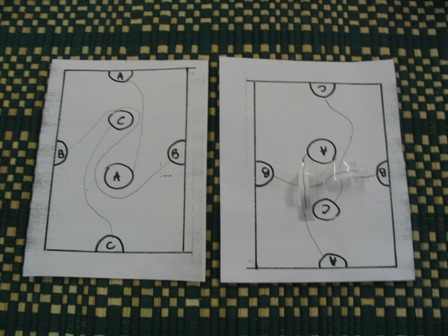
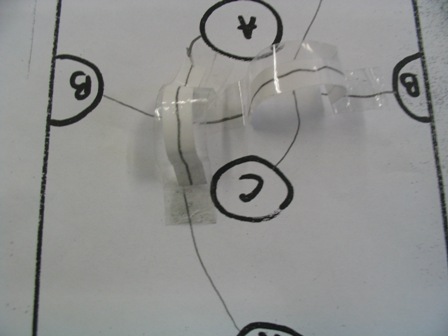
Az alábbi feladatmegoldás kitűnő példa a kreatív gondolkodásra. A feladat így szól: kösd össze A-t A-val, B-t B-vel és C-C-vel úgy, hogy az összekötő vonalak nem keresztezhetik egymást, nem lépnek ki a keretből, s nem mennek át a betűkön! Bal oldalon a szokásos, helyes megoldás látható. A mellette lévő képen Ny. Juli megoldása látható. Ő térben gondolkodva adott megoldást a problémára.
-
A kreatív gondolkodás tulajdonságai:
+
[[Kép:kreatív megoldás.jpeg]] [[Kép:kreatív megoldás közelebbről.jpeg]]
 +
 +
'''A kreatív gondolkodás tulajdonságai:'''
*kombináció, szintetizálás (a dolgok újra szétszedése, és összerakása)
*kombináció, szintetizálás (a dolgok újra szétszedése, és összerakása)
*alternatívák keresése (több lehetőség is lehet)
*alternatívák keresése (több lehetőség is lehet)
18. sor: 21. sor:
A kreativitás fejleszthető tantárgyi feladatokkal és gazdagító játékokkal. A '''gazdagító játék''' célzott fejlesztés során alkalmazott '''nem konkrét és direkt módon tantárgyhoz kötött tevékenység'''.
A kreativitás fejleszthető tantárgyi feladatokkal és gazdagító játékokkal. A '''gazdagító játék''' célzott fejlesztés során alkalmazott '''nem konkrét és direkt módon tantárgyhoz kötött tevékenység'''.
-
''Alternatívák keresése''
+
*'''''alternatívák keresése'' '''
Ilyesféle tantárgyi példákkal fejleszthetjük ezt a területet:
Ilyesféle tantárgyi példákkal fejleszthetjük ezt a területet:
30. sor: 33. sor:
''Hányféleképpen tudnád felírni az idei év évszámát? Próbáld sokféleképpen!
''Hányféleképpen tudnád felírni az idei év évszámát? Próbáld sokféleképpen!
2008, MMVIII, Kétezer-nyolc, 2000+8, 2009-1, stb.''
2008, MMVIII, Kétezer-nyolc, 2000+8, 2009-1, stb.''
 +
 +
Ugyanez közösségi játékként
 +
 +
''Valaki kölcsönkéri a labdátokat. Utasítsátok vissza!
 +
A nem, ne, se, nincs, sincs szavakat tilos használni.
 +
Ismételni nem lehet.
 +
(A gyerekek körben ülnek, hogy jól lássák egymást.)''
 +
 +
*'''''rugalmas nézőpontváltás (többféleképpen is meg közelíthető egy probléma)'''''
 +
 +
Tantárgyi példával
 +
 +
''Vágd fel a négyzetet 6, 7, 8 kisebb négyzetre!''
 +
 +
Gazdagító játékkal
 +
 +
''Hány kismajom bújt el a képen?
 +
 +
''Hány háromszög látható a képen?'' Képek, melyek többféleképp nézhetők; ábrák, melyek megtévesztik a gyanútlan nézőt.
 +
 +
*'''''visszalépés (a probléma lebontása alkotóelemeire)'''''
 +
Tantárgyi feladattal
 +
 +
''9 gyerek között úgy osztottunk szét 90 db almát, hogy a másodiktól kezdve minden gyerek annyival többet kapott az előzőnél, mint amennyit az első gyerek kapott. Hány almát kaptak fejenként?''
 +
 +
Gazdagító játékkal
 +
 +
''Robinson játék:
 +
Mit kell eltávolítani? Mi a felesleges? A teremben lévő egy-egy tárgyról mit kellene levenni, hogy másra használható legyen?''
 +
 +
*'''''határátlépés (divergens gondolkodás fejlesztése)'''''
 +
 +
Gazdagító játékkal
 +
 +
''Adott négy négyzet alakban elhelyezkedő pont. Rajzolj olyan háromszöget, melynek oldalain rajta van mind a négy pont.''
 +
 +
*'''''vizuális intelligencia és képzelet fejlesztése'''''
 +
 +
Tantárgyi feladattal
 +
 +
''Hány egyenest húzhatok az alábbi pontokon keresztül, ha egy egyenes legalább két ponton halad át?''
 +
 +
∙ ∙ ∙
 +
 +
∙ ∙ ∙
 +
 +
''11 egyenes húzható. A megoldáskor figyelembe kell venni a „legalább két ponton halad át” kifejezést, mely nem zárja ki a három ponton való áthaladást.''
 +
 +
 +
Gazdagító játékkal
 +
 +
Absztrakt rajz játék: a játékosok megpróbálnak olyan formákat, vonalakat rajzolni, amelyek semmilyen tárgyra nem hasonlítanak, az ellenfelek pedig értelmezik a látottakat. Négy-öt motívum után az ellenfelek elkezdhetik a felismerést. Pontot szerez, akinek a meglátását a többiek is elfogadják

Aktuális változat

A kreativitás alkotóképesség

Az alkotóképes ember tapasztalatait, meglévő tudását úgy tudja átrendezni, hogy újszerű problémát is meg tudjon oldani. Az alábbi feladatmegoldás kitűnő példa a kreatív gondolkodásra. A feladat így szól: kösd össze A-t A-val, B-t B-vel és C-C-vel úgy, hogy az összekötő vonalak nem keresztezhetik egymást, nem lépnek ki a keretből, s nem mennek át a betűkön! Bal oldalon a szokásos, helyes megoldás látható. A mellette lévő képen Ny. Juli megoldása látható. Ő térben gondolkodva adott megoldást a problémára.

Kép:kreatív megoldás.jpeg Kép:kreatív megoldás közelebbről.jpeg


A kreatív gondolkodás tulajdonságai:

  • kombináció, szintetizálás (a dolgok újra szétszedése, és összerakása)
  • alternatívák keresése (több lehetőség is lehet)
  • divergens gondolkodás (határátlépés: elrugaszkodás a megszokott megoldási sémáktól)
  • rugalmas nézőpontváltás (többféleképpen is meg közelíthető egy probléma)
  • átstrukturálás (a feladat átfogalmazása)
  • logika
  • visszalépés (a probléma lebontása alkotóelemeire)
  • vizuális intelligencia és képzelet
  • ötletesség

Gazdagító játékok

A kreativitás fejleszthető tantárgyi feladatokkal és gazdagító játékokkal. A gazdagító játék célzott fejlesztés során alkalmazott nem konkrét és direkt módon tantárgyhoz kötött tevékenység.

  • alternatívák keresése

Ilyesféle tantárgyi példákkal fejleszthetjük ezt a területet:

Egy kör alakú asztal mellett négy ember foglal helyet: Anna, Péter, Sára és Marci. Nincs asztalfő. a) Hányféle különböző ültetési lehetőség van? b) Anna ragaszkodik ahhoz, hogy Péter és Sára között üljön. Így hányféle lehetőség van?

Ugyanez gazdagító játékkal is megvalósítható.

Hányféleképpen tudnád felírni az idei év évszámát? Próbáld sokféleképpen! 2008, MMVIII, Kétezer-nyolc, 2000+8, 2009-1, stb.

Ugyanez közösségi játékként

Valaki kölcsönkéri a labdátokat. Utasítsátok vissza! A nem, ne, se, nincs, sincs szavakat tilos használni. Ismételni nem lehet. (A gyerekek körben ülnek, hogy jól lássák egymást.)

  • rugalmas nézőpontváltás (többféleképpen is meg közelíthető egy probléma)

Tantárgyi példával

Vágd fel a négyzetet 6, 7, 8 kisebb négyzetre!

Gazdagító játékkal

Hány kismajom bújt el a képen?

Hány háromszög látható a képen? Képek, melyek többféleképp nézhetők; ábrák, melyek megtévesztik a gyanútlan nézőt.

  • visszalépés (a probléma lebontása alkotóelemeire)

Tantárgyi feladattal

9 gyerek között úgy osztottunk szét 90 db almát, hogy a másodiktól kezdve minden gyerek annyival többet kapott az előzőnél, mint amennyit az első gyerek kapott. Hány almát kaptak fejenként?

Gazdagító játékkal

Robinson játék: Mit kell eltávolítani? Mi a felesleges? A teremben lévő egy-egy tárgyról mit kellene levenni, hogy másra használható legyen?

  • határátlépés (divergens gondolkodás fejlesztése)

Gazdagító játékkal

Adott négy négyzet alakban elhelyezkedő pont. Rajzolj olyan háromszöget, melynek oldalain rajta van mind a négy pont.

  • vizuális intelligencia és képzelet fejlesztése

Tantárgyi feladattal

Hány egyenest húzhatok az alábbi pontokon keresztül, ha egy egyenes legalább két ponton halad át?

∙ ∙ ∙

∙ ∙ ∙

11 egyenes húzható. A megoldáskor figyelembe kell venni a „legalább két ponton halad át” kifejezést, mely nem zárja ki a három ponton való áthaladást.


Gazdagító játékkal

Absztrakt rajz játék: a játékosok megpróbálnak olyan formákat, vonalakat rajzolni, amelyek semmilyen tárgyra nem hasonlítanak, az ellenfelek pedig értelmezik a látottakat. Négy-öt motívum után az ellenfelek elkezdhetik a felismerést. Pontot szerez, akinek a meglátását a többiek is elfogadják

A lap eredeti címe "http://alsos.fazekas.hu/wiki/Kreativit%C3%A1s"